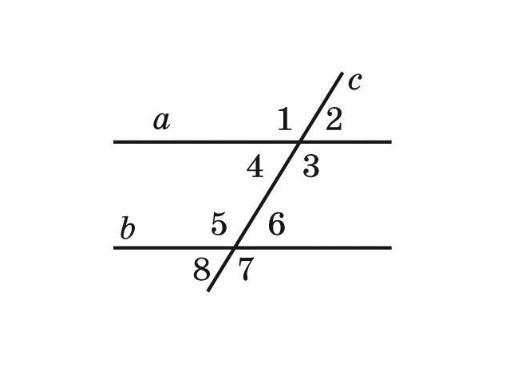Question

Знайдіть усі кути, утворені при перетині двох прямих січною, якщо
відомо, що один з них відноситься до іншого як 2 до 3.

Answer 1

Ответ:

∠1=∠3=∠5=∠7=108°

∠2=∠4=∠6=∠8=72°

Объяснение:

Знайдіть усі кути, утворені при перетині двох прямих січною, якщо

відомо, що один з них відноситься до іншого як 2 до 3

Якщо дві прямі а і b перетнути третьою прямою с, то утвориться 8 кутів.

∠3 і ∠6, ∠4 і ∠5 називають внутрішніми односторонніми

∠3 і ∠5, ∠4 і ∠6 називають внутрішніми різносторонніми

∠6 і ∠2, ∠5 і ∠1, ∠3 і ∠7, ∠4 і ∠8 назівають відповідними.

Властивості кутів, які утворюються при перетині двох паралельних прямих із третьою (січною):

• різносторонні кути рівні;

• відповідні кути рівні;

• сума односторонніх кутів дорівнює 180°.

Розв'язування:

    Серед кутів, що утворилися при перетині двох паралельних прямих січною і не є рівними, суміжні і внутрішні односторонні. Однак і ті, й інші кути в сумі дорівнюють 180°.

   Нехай градусна міра одного з внутрішніх односторонніх кутів 2х, тоді градусна міра другого — 3х. Оскільки їх сума дорівнює 180°, маємо:

∠6+∠3=180°

2х+3х=180°

5х=180°

х=36°

Отже:

∠6=2·36°=72°,

∠3=3·36°=108°

∠5=∠3=108° (як внутрішні різносторонні кути)

∠4=∠6=72° (як внутрішні різносторонні кути)

∠1=∠5=108° (як відповідні кути)

∠2=∠6=72° (як відповідні кути)

∠7=∠3=108° (як відповідні кути)

∠8=∠4=72° (як відповідні кути)

#SPJ1