Предмет: Математика,
автор: Cudlesss
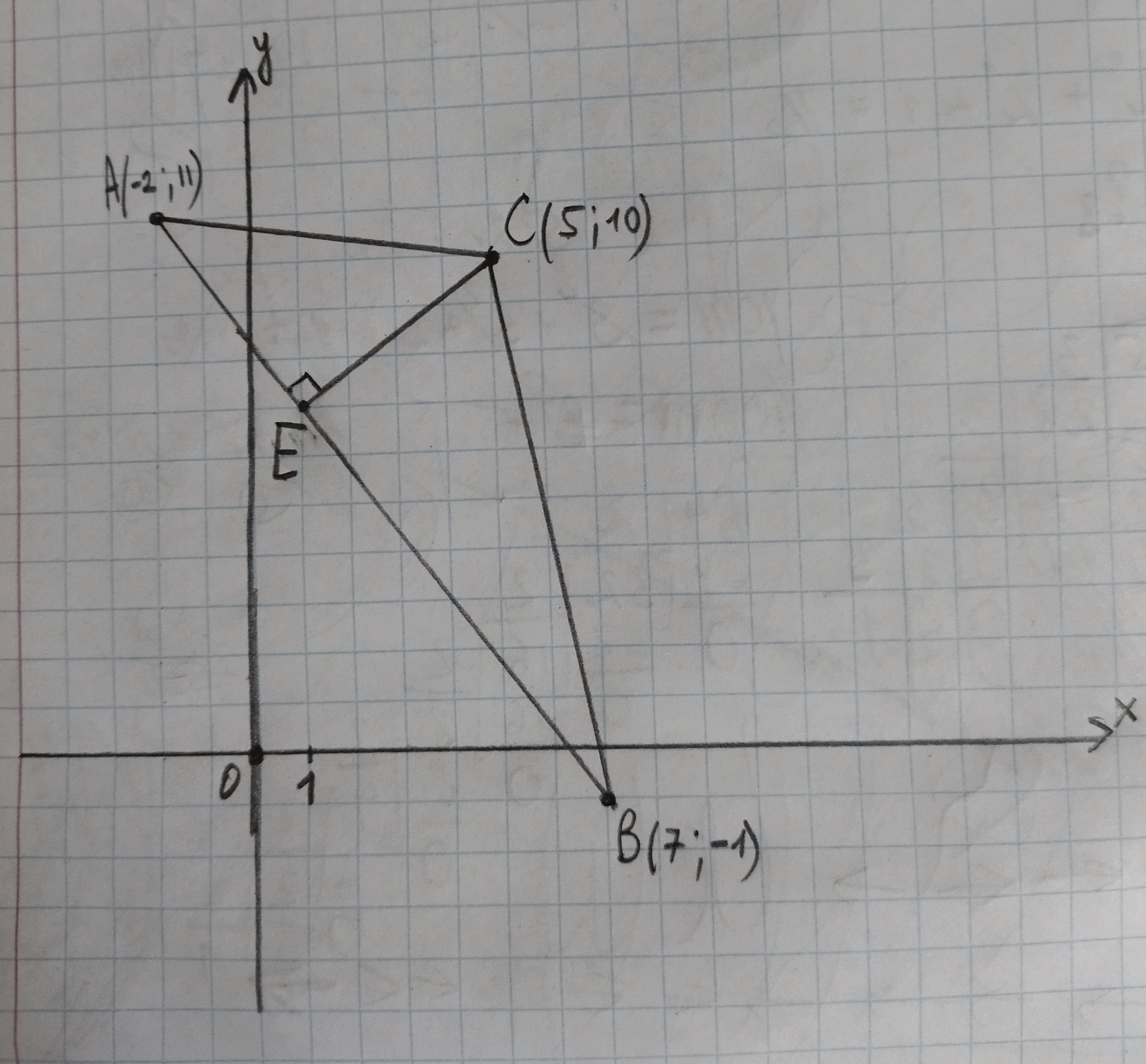
Дано точки A(-2;11), B(7:-1), C(5;10). CE-висота трикутника. Знати точку Е.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Е ( 1; 7)
Пошаговое объяснение:
Даны точки А( -2;11) , В(7; -1) , С (5; 10) . СЕ - высота треугольника . Найти координаты точки Е .
Составим уравнение прямой АВ.
Прямую можно задать уравнением.
Подставим в данное уравнение координаты точек А и В и решим систему уравнений
Тогда получим уравнение прямой АВ
Если СЕ - высота Δ АВС, СЕ ⊥АВ .
Найдем угловой коэффициент прямой СЕ из условия перпендикулярности.
Составим уравнение прямой СЕ
Так как точка С принадлежит этой прямой, то подставим координаты этой точки и найдем значение b
Тогда уравнение прямой СЕ
Точка Е -точка пересечения прямых АВ и СЕ . Найдем абсциссу точки пересечения, решив уравнение
Найдем ординату данной точки
Значит, точка Е ( 1; 7)
#SPJ1
Похожие вопросы
Предмет: Математика,
автор: sofzww
Предмет: Алгебра,
автор: shkvarenkoehor
Предмет: Алгебра,
автор: shkvarenkoehor
Предмет: Информатика,
автор: talkush88
Предмет: Другие предметы,
автор: terrayurima19