50 балов герою Алгебра 4 системы
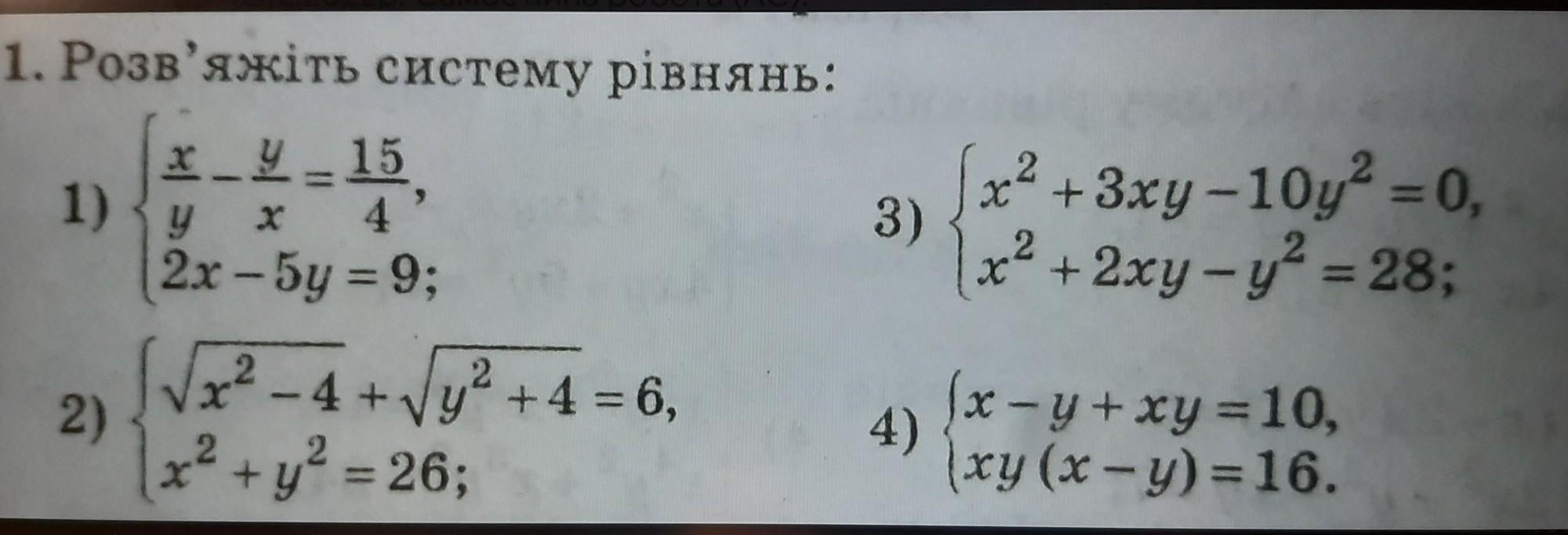
Ответы
Ответ:
1) ( 12 ; 3 ) , ( -0,5 ; -2)
2) (√5 ; √21 ) , (-√5 ; √21) , (√5 ; -√21 ) , (-√5 ; -√21 )
3) ( 2 ; 4 ) , (-2 ; -4) , (√2 ; -√5) , (-√2 ; √5)
4) (3√2 ; -8 + 3√2) , (-3√2 ; -8 - 3√2) , (4 ; 2 ) , ( -2 ; -4)
Объяснение:
№1
Рассмотрим первое уравнение системы
За счет симметрии мы можем ввести замену
Теперь мы должны рассмотреть два случая :
Подставим получившееся выражение в рамке , во второе уравнение системы
Аналогично
Данная система имеет два решения
( 12 ; 3 ) , ( -0,5 ; -2)
№2
ОДЗ :
Из второго уравнения системы
Подставляем в первое уравнение системы
ОДЗ :
Возводим обе части в квадрат
Снова возводим в квадрат
Уравнение в первой скобке не имеет действительных корней , а во а во второй имеет
Оба корня принадлежат промежутку
Находим x , рассмотрев два случая
Первый
Оба корня удовлетворяют ОДЗ
Второй
Таким образом данная система имеет 4 симметричных решения
(√5 ; √21 ) , (-√5 ; √21) , (√5 ; -√21 ) , (-√5 ; -√21 )
№3
Рассмотрим первое уравнение системы
Подставим x = 2y второе уравнение системы
Теперь подставим x = -5y
Данная имеет 4 решения
( 2 ; 4 ) , (-2 ; -4) , (√2 ; -√5) , (-√2 ; √5)
№4
Введем замену
И мы получим :
В данном случае можно подобрать корни как в Теореме Виета
По итогу данная система будет иметь 4 решения
(3√2 ; -8 + 3√2) , (-3√2 ; -8 - 3√2) , (4 ; 2 ) , ( -2 ; -4)
#SPJ1