4. В квадрате ABCD на продолжении стороны AD за точку А выбрана точка F так, что <BCF = 2LACF. Периметр квадрата равен 4 см. Найти длину отрезка КС.
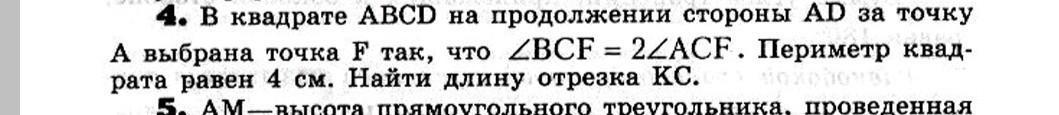
Ответы
Ответ:
см.
Объяснение:
В квадрате АВСD на продолжении стороны А за точку А выбрана точка F так , что∠BCF =∠2 ∠ACF . Периметр квадрата равен 4 см. Найти длину отрезка КС.
Так как в условии не сказано, где точка К , то предполагаю, что это точка пересечения С F стороны АВ.
Рассмотрим рисунок. Проведем диагональ АС . По условию
∠BCF=∠2 ∠ACF . Пусть ∠ACF =α. Тогда ∠BCF = 2α.
Отсюда ∠АСВ = 3α. Диагонали квадрата являются биссектрисами углов. Все углы квадрата по 90°. Тогда 3α= 45°. Отсюда α= 15°.
Значит, ∠BCF = 2α= 30°.
Так как периметр квадрата равен 4 см, у квадрата все стороны равны, то сторона квадрата равна 1 см.
Рассмотрим Δ СВК - прямоугольный, ВС = 1см, ∠BCF = 30°.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
см
#SPJ1