Question

Срочно!!! Очень нужно

Answer 1

Ответ:

1) См. решение

2) D(y) = (4; +∞)

3) График пересекает ось Ох в точке (-1,5; 0);

График пересекает ось Оу в точке (0; -1)

Объяснение:

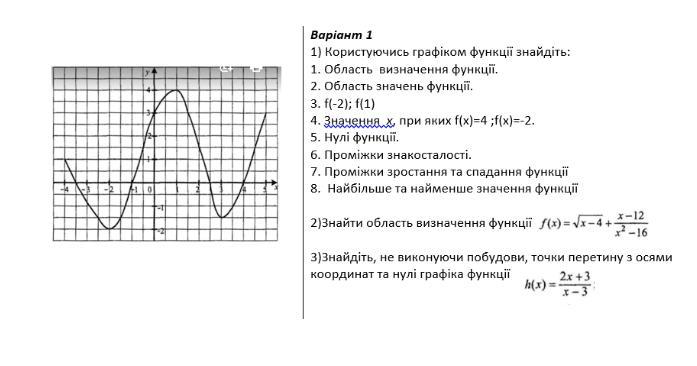
1) Пользуясь графиком функции найдите:

1. Область определения функции.

2. Область значений функции.

3. f(-2); f(1)

4. Значениях, при которых f(x)=4; f(x)=-2.

5. Нули функции.

6. Промежутки постоянства знака.

7. Промежутки возрастания и убывания функции

8. Наибольшее и наименьшее значение функции

2) Найти область определения функции $\displaystyle f(x)=\sqrt{x-4} +\frac{x-12}{x^2-16}$

3) Найдите, не выполняя построения, точки пересечения с осями координат и нули графика функции

$\displaystyle h(x)=\frac{2x+3}{x-3}$

1) Пользуясь графиком функции найдите:

1. Область определения функции.

- все допустимые значения аргумента.

D(y) = [-4; 5]

2. Область значений функции.

- все значения функции на области определения.

Е(у) = [-2; 4]

3. f(-2); f(1)

Находим данные точки на оси Ох, проводим перпендикуляр до пересечения с графиком, из точек пересечения опустим перпендикуляр на Оу и определяем значения функции.

f(-2) = -2, f(1) = 4

4. Значениях, при которых f(x)=4; f(x)= -2.

f(x)=4 ⇒ х = 1;

f(x)= -2 ⇒ х = -2.

5. Нули функции.

- точки, в которых график пересекает Ох, то есть у = 0.

у = 0 при х = {-3,5; -1; 2,5; 4}

6. Промежутки постоянства знака.

y > 0 при х ∈ [-4; -3,5) ∪ (-1; 2,5) ∪ (4; 5]

y < 0 при х ∈ (-3,5; -1) ∪ (2,5; 4)

7. Промежутки возрастания и убывания функции.

Функция возрастает на промежутках: [-2; 1], [3; 5].

Функция убывает на промежутках: [-4; -2], [1; 3].

8. Наибольшее и наименьшее значение функции.

у наиб. = 4; у наим. = -2.

2) Найти область определения функции $\displaystyle f(x)=\sqrt{x-4} +\frac{x-12}{x^2-16}$

1. Подкоренное выражение неотрицательно.

⇒ х - 4 ≥ 0

x ≥ 4

2. На ноль делить нельзя.

⇒ x² - 16 ≠ 0

(x - 4)(x + 4) ≠ 0

x ≠ 4; x ≠ -4

⇒ D(y) = (4; +∞)

3) Найдите, не выполняя построения, точки пересечения с осями координат и нули графика функции

$\displaystyle h(x)=\frac{2x+3}{x-3}$

1. График пересекает ось Ох.

⇒ у = 0

Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля.

⇒ х ≠ 3

$\displaystyle 0=\frac{2x+3}{x-3}\\\\2x+3=0\\\\x=-1,5$

График пересекает ось Ох в точке (-1,5; 0)

⇒ h(x) = 0 при х = -1,5

- это и будет нулем данной функции.

2. График пересекает ось Оу

⇒ х = 0

$\displaystyle h(0)=\frac{0+3}{0-3}=-1$

График пересекает ось Оу в точке (0; -1)

#SPJ1