Предмет: Математика,
автор: bokutoku11
ПОМОГИТЕ ПОЖАЛУЙСТА!
Приложения:

Ответы
Автор ответа:
2
3. Ответ : 0
4. Ответ : 4,5 (ед)²
5. Ответ : 68 м
Пошаговое объяснение:
3. Вычислите интеграл :
Применяем формулу Ньютона-Лейбница :
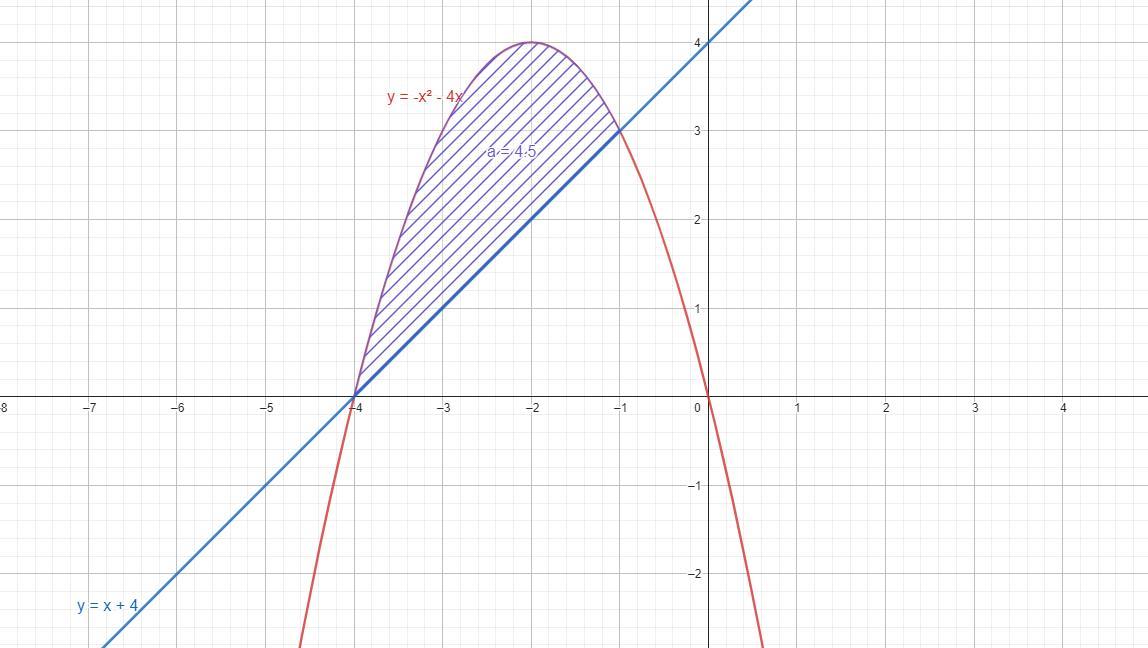
4. Вычислите площадь фигуры которая ограничена линиями :
y = -x² -4x , y = 4 + x
Находим точки пересечения данных графиков
-x² -4x = x + 4
x² + 5x + 4 = 0
(x+1)(x+4) = 0
x₁ = - 1 , x₂ = -4
Находим площадь данной фигуры :
5. Тело движется прямолинейно со скоростью v(t) = 3t² +1 (м/c) Найдите путь, пройденный телом за промежуток времени от
t = 1 (c) , t = 4(c)
Согласно механическому смыслу производной :
В нашем случае t = 0 , t = 4 пределы интегрирования
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vovaperepolkin
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: hhhg36361
Предмет: Биология,
автор: shahruh1507
Предмет: Математика,
автор: sabinahgfd