Question

Найдите точку пересечения прямых
4(x-3)+3(y+2)=-12 и 5(x+1)+y=14.

Answer 1

Ответ:

x, y = {3, -6}

Пошаговое объяснение:

Можно просто решить систему уравнений и найти x, y. А можно решить эту задачу графически.

1. Решение системы:

$\left \{ {{4(x-3)+3(y+2)=-12} \atop {5(x+1)+y=14}} \right. \\\left \{ {{4x-12+3y+6+12=0} \atop {y=14-5x-5}} \right. \\\left \{ {{4x+3y+6=0} \atop {y=9-5x}} \right. \\\left \{ {{4x+3(9-5x)+6=0} \atop {y=9-5x}} \right. \\\left \{ {{4x+27-15x+6=0} \atop {y=9-5x}} \right. \\\left \{ {{x=3} \atop {y=-6}} \right.$

Точка пересечения прямых: x, y = {3, -6}

2. Графическое решение:

Повторяем первые два действия как в прошлом решении, а затем из обоих уравнений выражаем y:

$y=\frac{-6-4x}{3} \\y=9-5x$

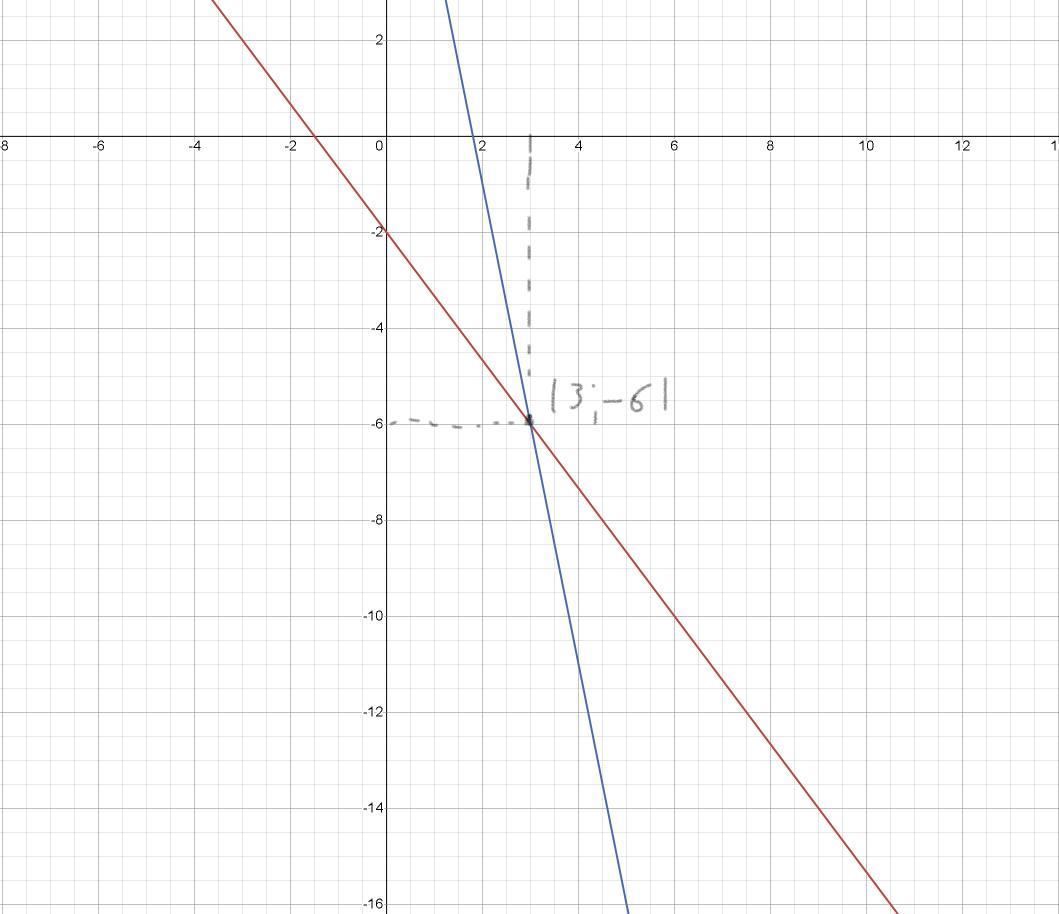
Чертим два графика и находим их пересечение. Я прикрепил файл, там это можно увидеть:

Точка пересечения прямых: x, y = {3, -6}