Предмет: Алгебра,
автор: baunti13
Допоможіть!!! Алгебра. Спростіть вираз, знайдіть його значення
Приложения:
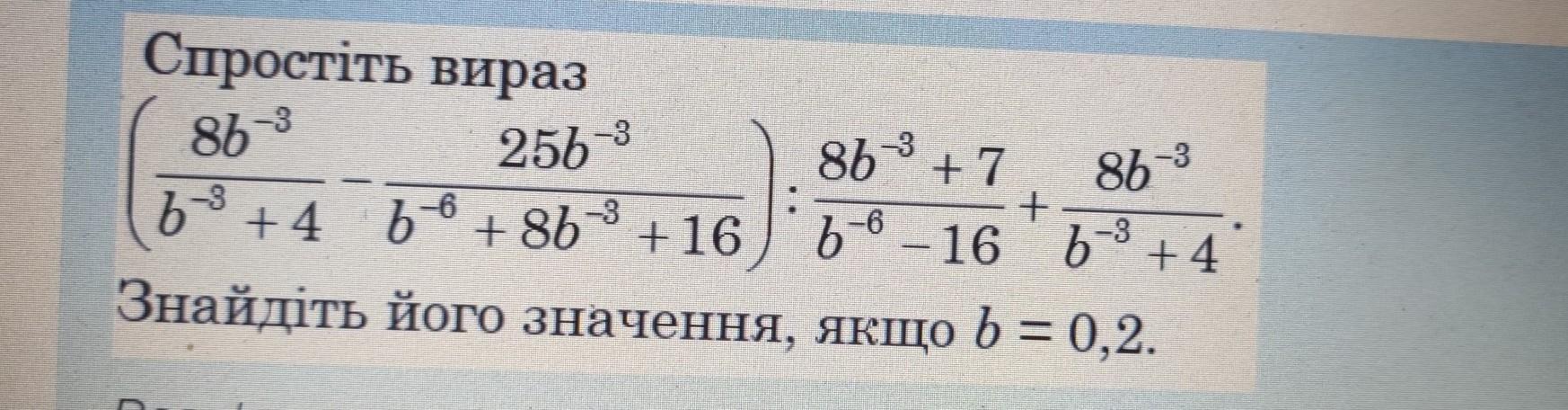
Ответы
Автор ответа:
1
Відповідь: 125
Пояснення:
розв'язання завдання додаю
Приложения:

baunti13:
Дякую!
Автор ответа:
1
Ответ:
125
Объяснение:
Будем использовать свойства степеней:
Решаем:
Подставляем в наше уравнение b = 0.2:
Похожие вопросы
Предмет: Українська мова,
автор: evhenvernyhora
Предмет: Химия,
автор: petaafanasov64
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: komiljonobloqulov
Предмет: Физкультура и спорт,
автор: dodykalova