Question

В треугольнике ABC, где A[-3; -1], B [5; 1], C [5; 6], вычислите размеры
внутренние углы. Проверьте графически.

Answer 1

В треугольнике ABC, где A[-3; -1], B [5; 1], C [5; 6], вычислите размеры внутренние углы.

Находим координаты векторов.

АВ = (5-(-3); 1-(-1) = (8; 2), модуль равен √(64+4) = √68 = 2√17.

ВС = (5-5); 6-1) = (0; 5), модуль равен √(0+25) = √25 = 5.

АС = (5-(-3); 6-(-1)) = (8; 7), модуль равен √(64+49) = √113 .

Угол A между векторами a и b определяем по формуле:

cos A = (x(a)*x(b) + (y(a)*y(b)) / (|a|*|b|).

Подставив данные, получаем:

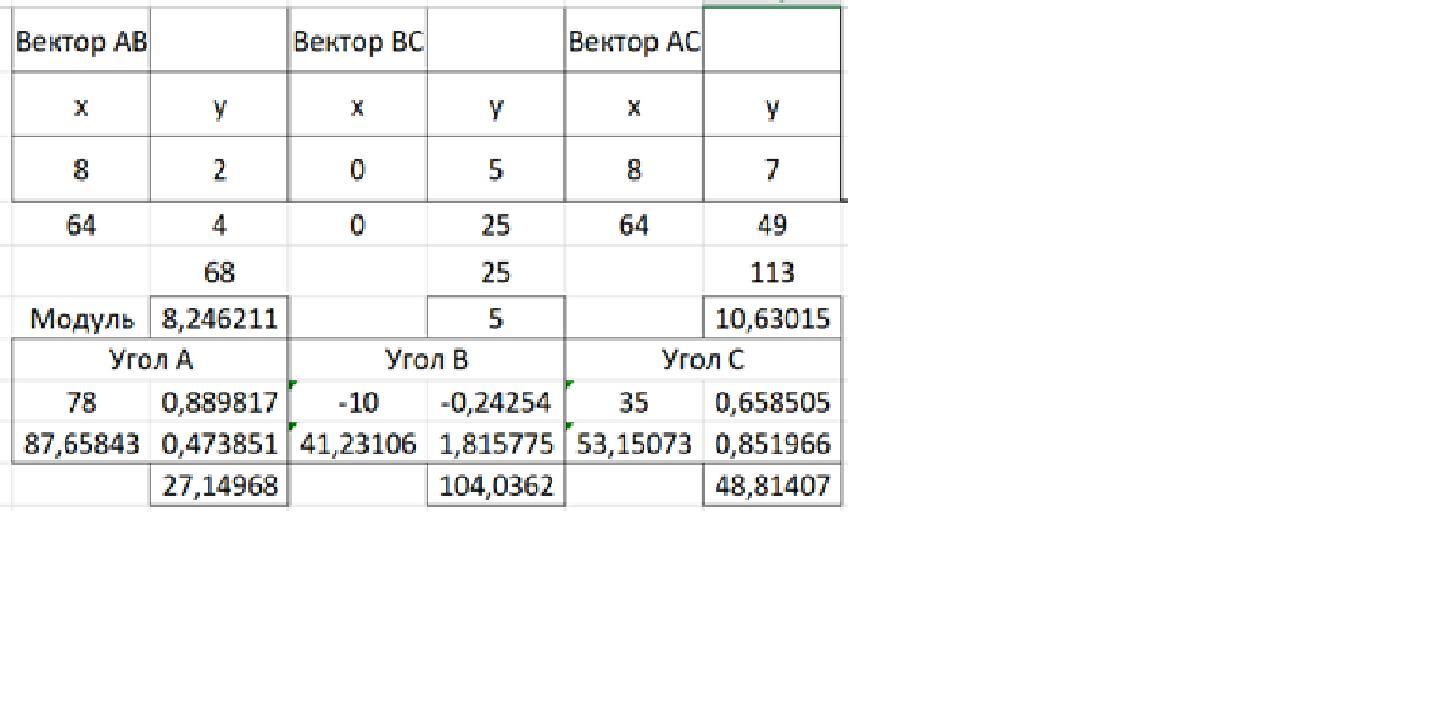
Вектор АВ  Вектор ВС  Вектор АС

х у х у х у

8 2 0 5 8 7

64 4 0 25 64 49

68  25  113

Модуль 8,246211251        5              10,63014581

Угол А                               Угол В                              Угол С

78 0,889817463 -10 -0,242535625 35 0,658504608

87,658428 0,473851336 41,23105626 1,81577499 53,15072906 0,851966327

27,1496817°  104,0362435°  48,81407483°

Из-за плохого форматирования с программы Excel даётся копия.