Предмет: Геометрия,
автор: samsunglilya1985
З точки яка віддалена від площини на а, проведено дві похилі під кутом 30 градусів до площини, причому їх проекції утворюють кут 45 градусів. Знайдіть відстань між основами похилих , якщо кут між їх проекціями = 120 градусів .
samsunglilya1985:
З точки яка віддалена від площини на а, проведено дві похилі під кутом 30 градусів до площини. Знайдіть відстань між основами похилих , якщо кут між їх проекціями = 120 градусів .
Ответы
Автор ответа:
2
Ответ:
Расстояние между основаниями наклонных равно 3а.
Объяснение:
Из точки, которая удалена от плоскости на а, проведены две наклонные под углом 30 градусов к плоскости. Найдите расстояние между основаниями наклонных, если угол между их проекциями равен 120 градусов .
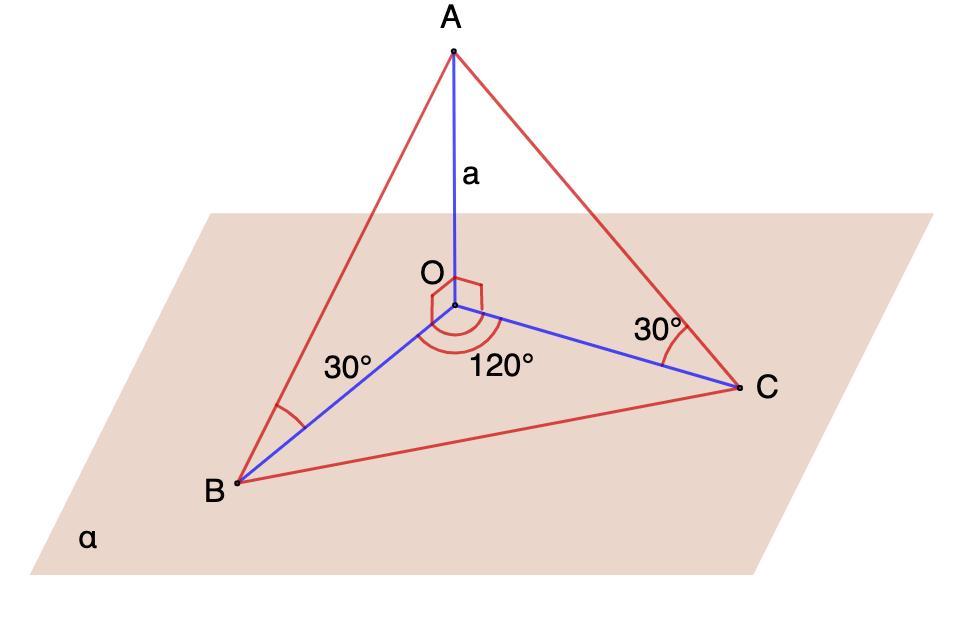
Дано: А ∉ α;
АВ и АС - наклонные;
АО = а; ∠АВО = ∠АСО = 30°;
∠ВОС = 120°
Найти: ВС.
Решение:
Рассмотрим ΔВАО и ΔОАС - прямоугольные.
∠АВО = ∠АСО = 30° (условие)
АО - общая.
ΔВАО = ΔОАС (по катету и острому углу)
⇒ ОВ = ОС (соответственные элементы)
Рассмотрим ΔВАО - прямоугольный.
- Котангенс угла - отношение прилежащего катета к противолежащему.
Рассмотрим ΔВОС.
ОВ = ОС = а√3; ∠ВОА = 120°
Теорема косинусов:
- Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Расстояние между основаниями наклонных равно 3а.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Биология,
автор: idk46
Предмет: Другие предметы,
автор: svistunbogdan
Предмет: Геометрия,
автор: Аноним
Предмет: Немецкий язык,
автор: rromantika
Предмет: Русский язык,
автор: Netvoy