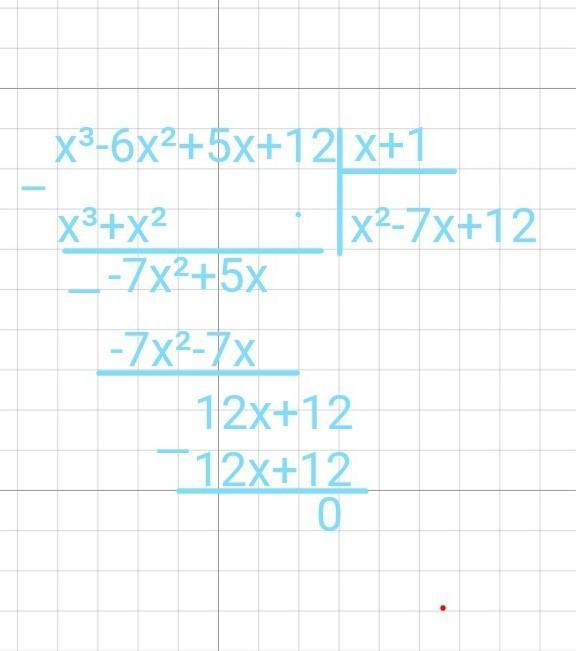Question

Решить уравнение: $x^3-6x^2+5x+12=0.$ Как решить его рациональнее? Честно говоря, метод разложения на множители мне не совсем подходит, поскольку мне сложно привести исходной многочлен к такому виду, в котором можно будет вынести общий множитель за скобки...

Answer 1

Ответ:

x = {-1, 3, 4}

Объяснение:

Если вам не подходит метод разложения, то можно воспользоваться методом подбора рациональных корней. Он очень ситуативный и в отдельных случаях не всегда подойдёт, но попробовать можно.

Будем работать с коэффициентами a = 1, b = - 6, c = 5, d = 12.

1. Если a + b + c + d = 0, то уравнение имеет корень x = 1.

Нам это не подходит.

2. Если b + d = a + c, то уравнение имеет корень x = -1.

Так как -6 + 12 = 1 + 5, значит наше уравнение имеет корень -1.

3. Так как a, b, c, d - целые числа, то можно попробовать подобрать такие рациональные корни p / q, что d будет нацело делится на p, а a будет нацело делится на q.

В общем случае, это простое нахождение корней среди делителей свободного члена, так как у нас a = 1.

Рассмотрим делители числа 12: {1, 2, 3, 4, 6, 12}.

Сразу можно отсеять числа 1, 12, так как они нам не подойдут. Теперь просто подставляем остальные числа и находим остальные корни:

x = 3, 4

• Любое кубическое уравнение с действительными коэффициентами имеет по крайней мере один действительный корень, два других либо также действительные, либо являются комплексно сопряженной парой.

Мы нашли 3 действительных корня, они и являются решением нашего уравнения.

Данный способ не будет работать, если уравнение имеет иррациональные корни.

Answer 2

$\displaystyle x^3-6x^2+5x+12=0$

• Обратим внимание на последнее слагаемое(12) и запишем его делители: ±1;±2;±3...

• Подставим эти делители вместо х-ов в уравнение и проверим, при каком из этих значений уравнение станет верным. И то значение, которое нам подойдет, будет одним из действительных корней, который решит данное уравнение. Далеко не пойдя поймём, что -1 является одним из действительных корней.

• Теперь самое основное – делим наше уравнение на х "минус" на этот же корень(-1). Т.е. на х+1. После деления получим ответ без остатков, значит произведение частного и делителя равняются нашему исходному уравнению. Т.е. вместо нашего кубического многочлена можем записать: (х+1)(х²-7х+12) = 0.

• Вторую скобку разложим на множители: (х+1)(х-3)(х-4) = 0. Отсюда выходит, что корни -1; 3; 4 решат данное уравнение.

Ответ: х₁ = -1, х₂ = 3, х₃ = 4