Предмет: Математика,
автор: alewa22222
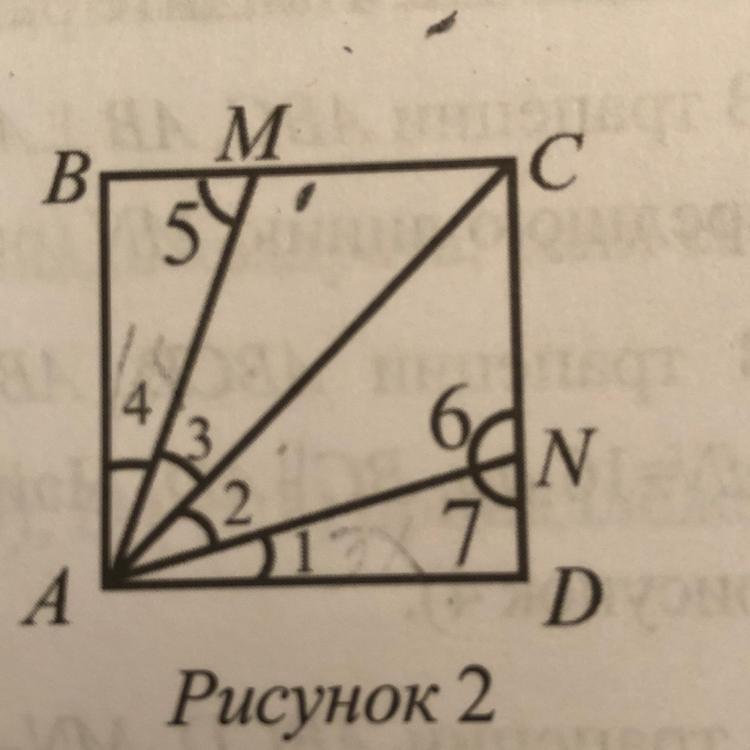
В квадрате АБЦД,<3=3•<2,
<1:<4=11:3.Найдите разность <5-<7
Приложения:
Ответы
Автор ответа:
0
Ответ:
Разность ∠5 - ∠7 = 24°.
Пошаговое объяснение:
В квадрате АВСD: ∠3 = 3·∠2; ∠1 : ∠4 = 11 : 3. Найти разность ∠5 - ∠7.
Дано: АВСD - квадрат.
∠3 = 3·∠2; ∠1 : ∠4 = 11 : 3
Найти: ∠5 - ∠7
Решение:
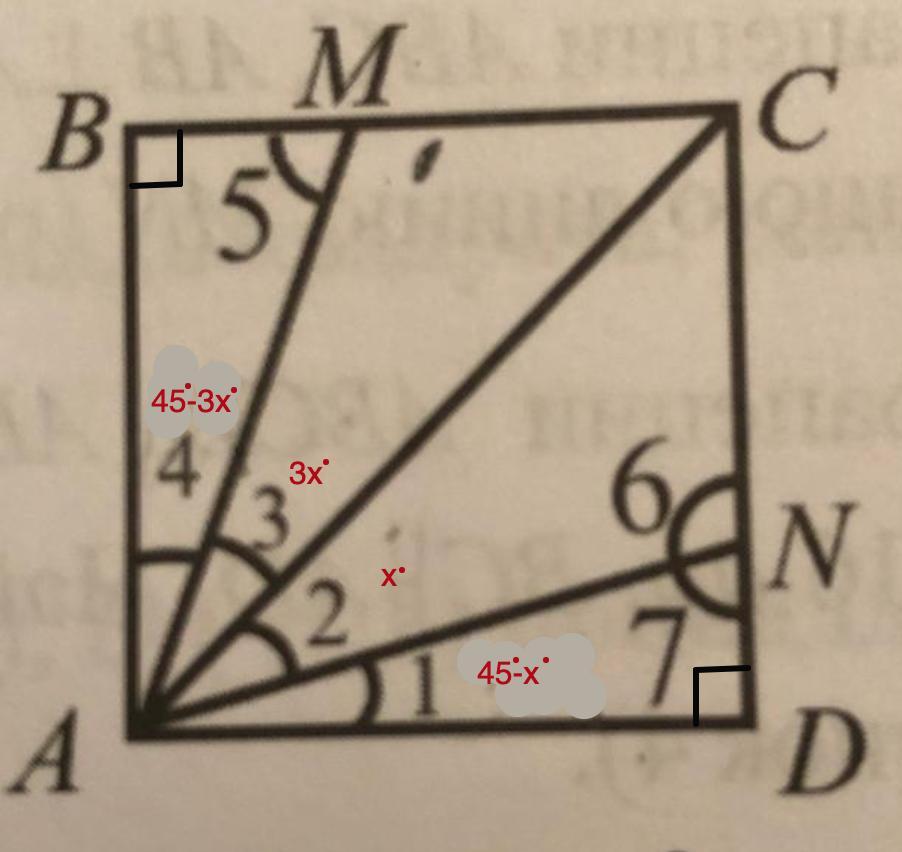
Пусть ∠2 = х, тогда ∠3 = 3х.
- Диагонали квадрата являются биссектрисами его углов.
⇒ ∠ВАС = ∠CAD = 90° : 2 = 45°
⇒ ∠4 = 45° - ∠3 = 45° - 3х
∠1 = 45° - ∠2 = 45° - х
По условию ∠1 : ∠4 = 11 : 3
- Основное свойство пропорции: произведение средних членов равно произведению крайних.
∠4 · 11 = ∠1 · 3
Подставим значения и решим уравнение:
(45 - 3х) · 11 = (45 - х) · 3
495 - 33х = 135 - 3х
-30х = -360 |:(-30)
x = 12
⇒ ∠2 = 12°;
∠3 = 36°;
∠1 = 45° - 12° = 33°;
∠4 = 45° - 36° = 9°.
ΔАВМ - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠5 = 90° - ∠4 = 90° - 9° = 81°
ΔAND - прямоугольный.
∠7 = 90° - ∠1 = 90° - 33° = 57°
Найдем разность:
∠5 - ∠7 = 81° - 57° = 24°
Приложения:
Похожие вопросы
Предмет: Физика,
автор: bolotovaliza108
Предмет: Химия,
автор: andriykaymakov
Предмет: Английский язык,
автор: kradchenko2018
Предмет: Геометрия,
автор: Koneshkno
Предмет: Математика,
автор: armybtsforever1393