Question

Через вершину прямого кута C трикутника ABC до його площини проведено перпендикуляр ск. відстань від точки К до прямої AB дорівнює 13 см. Знайдіть відстань від точки к до площи трикутника,якщо його катети дорівнюють 15см і 20 см

Answer 1

Через вершину прямого угла C треугольника ABC к его плоскости проведен перпендикуляр ск. расстояние от точки К до прямой AB равно 13 см. Найдите расстояние от точки к до площади треугольника, если его катеты равны 15см и 20см.

------------------------------------------------------

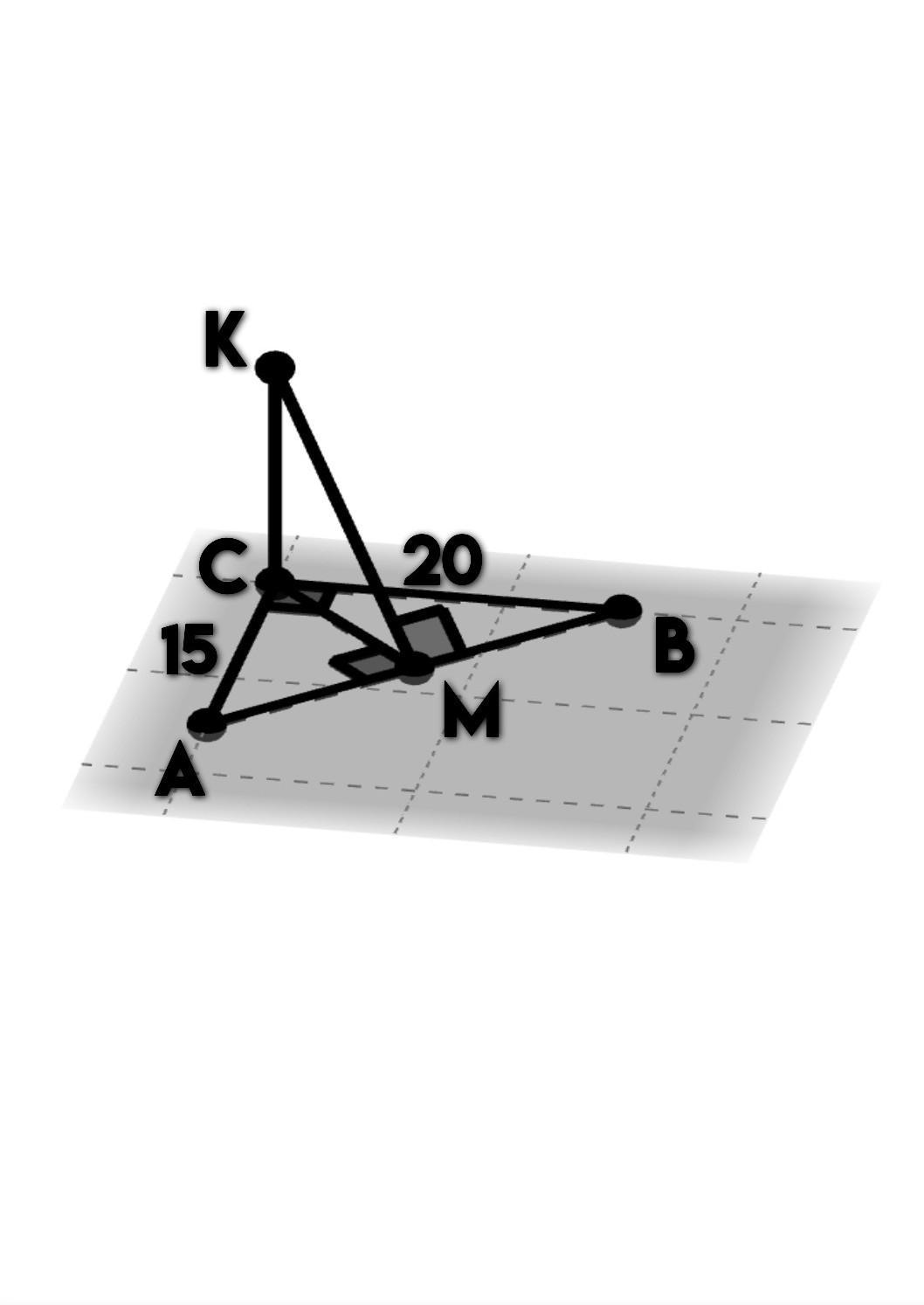
Дано: ∆АВС, СК ⟂ (АВС), Р(К;АВ) = 13см, ∠С = 90°, АС = 15см, ВС = 20см.

Найти: Р(К;(АВС))

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Расстояние от точки до плоскости - это перпендикуляр, опущенный из данной точки на плоскость. Р(К;(АВС)) = СК.
• Расстояние от точки К до прямой АВ - перпендикуляр МК, равный 13см(по условию). Гипотенуза ∆АВС согласна Т. Пифагора равна:

АВ =√(АС² + ВС²)

АВ = √(225+400)

АВ = √625

АВ = 25см.

• В ∆АВС опустим высоту на гипотенузу, которая равна произведению катетов, деленное на эту же гипотенузу.

$\displaystyle \boldsymbol{CM = \frac{AC \,*\,BC}{AB} }$

$\displaystyle \boldsymbol{ \: CM = \frac{15 \,*\,20}{25} = 12cm}$

• Рассмотрим ∆КСМ. СК - искомый. По теореме Пифагора:

СК = √(КМ²-СМ²)

СК = √(169-144)

СК = √25

СК = 5см

Ответ: Р(К;(АВС)) = 5см