Знайти кут між прямою
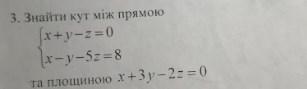
Ответы
Находим направляющий вектор N заданной прямой как векторное произведение нормальных векторов плоскостей, задающих прямую.
i j k | i j
1 1 -1 | 1 1
1 -1 -5 | 1 -1 = -5i – 1j -1k + 5j- 1i – 1k =-6i + 4j – 2k,
N = (-6; 4; -2).
Теперь находим координаты точки, принадлежащей прямой, как решение системы из уравнений плоскостей.
Но так как имеем два уравнения с тремя переменными, то примем одну из них, а именно z = 0.
{x + y – 0 = 0
{x - y – 5*0 + 8 = 0
2x + 8 = 0, x = -8/2 = -4, y = -x = 4.
Получили точку А(-4; 4; 0).
Уравнение прямой преобразовано в каноническое:
(x + 4)/(-6 )= (y – 4)/4 = z/(-2) или, сократив на (-2)
(x + 4)/3= (y – 4)/(-2) = z/1.
Найдем угол между прямой (x+4)/3=(y-4)/(-2)=z/1 и плоскостью
x + 3 y - 2 z = 0
Направляющий вектор прямой имеет вид:
s
= { 3 ; -2 ; 1 }
Вектор нормали плоскости имеет вид:
q
= { 1 ; 3 ; -2 }
Угол между прямой и плоскостью:
sin φ=
| A · l + B · m + C ·n | =
√(A² + B² + C²) ·√(l² +m² + n²)
= | 1 · 3 + 3 · (-2) + (-2) · 1 | =
√(1² + 3² + (-2)²) · √(3² + (-2)² + 1²)
= | 3 - 6 - 2|
√(1 + 9 + 4) · √(9 + 4 +1)
= 5/14 ≈ 0.357143.
Отсюда угол равен arcsin(5/14) = 20,9248 градуса.