Question

Допоможіть будь ласка.
Дякую.

Answer 1

Ответ:

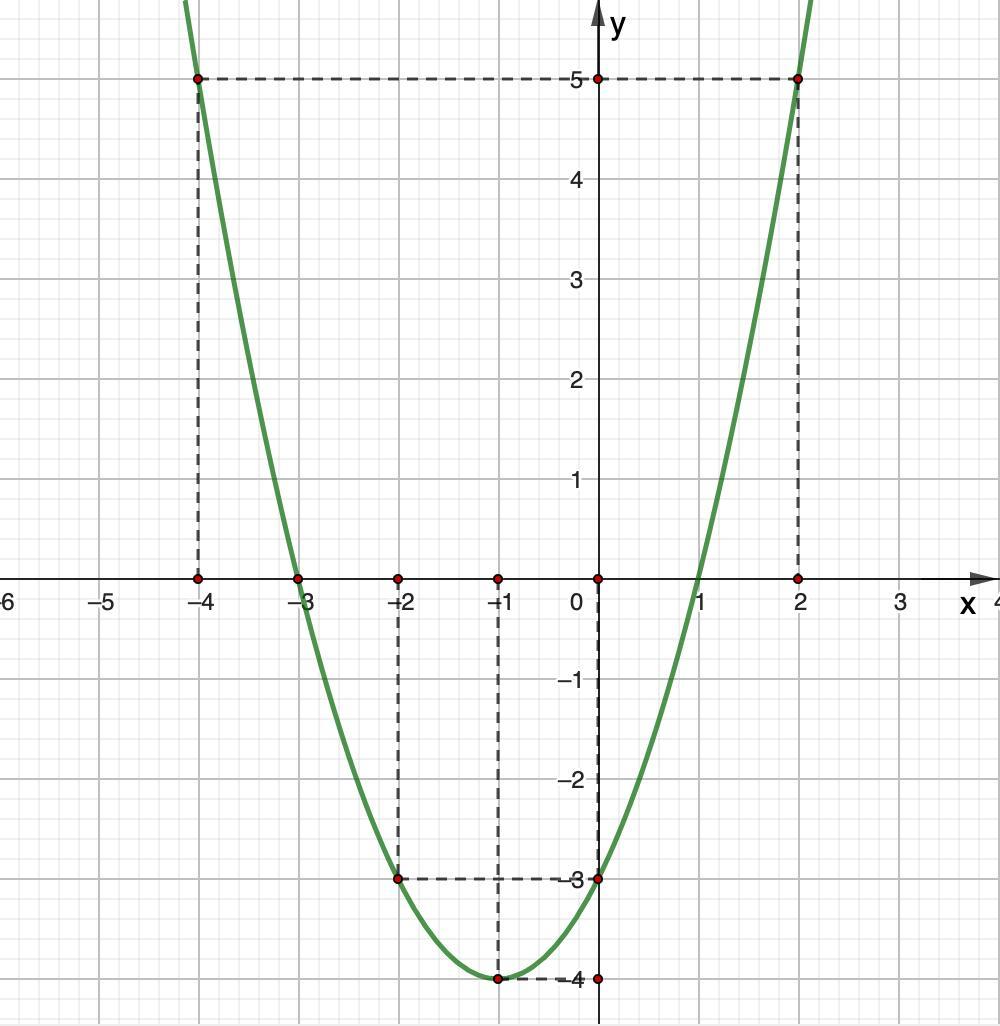
1) Координаты вершины параболы (-1; -4)

2) D(y) = x ∈ R; E(y) = y ∈ [-4; +∞)

3) 1 > 0 ⇒ ветви вверх.

4) у = 0 при х₁ = -3; х₂ = 1

5) y > 0 при х ∈ (-∞; -3) ∪ (1; +∞)

y < 0 при х ∈ (-3; 1)

6) функция убывает при х ∈ (-∞; -1]

функция возрастает при х ∈ [-1; +∞)

7) у наим. = -4

Наибольшего значения функция не имеет (+∞)

8) график построен.

Объяснение:

8.Исследуйте функции f (x) = 2х-3+х². По схеме:

1) Найдите вершину параболы.

2) Область определения и область значения.

3) Направление ветвей.

4) Нули функции.

5) Промежутки знакопостоянства.

6) Промежутки возрастания и убывания.

7) Наибольшее и наименьшее значение функции.

8) Нарисуйте точный график данной функции.

Дана функция:  f(x) = 2х - 3 + х²   или  f(x) = x² + 2x - 3

- квадратичная функция вида у = ax² + bx + c, график парабола, a > 0 ⇒ ветви вверх.

1) Найдите вершину параболы.

Абсциссу вершины параболы найдем по формуле:

$\displaystyle \bf x_0=-\frac{b}{2a}$

$\displaystyle x_0=-\frac{2}{2}=-1$

$\displaystyle y_0=(-1)^2+2\cdot (-1)-3=-4$

Координаты вершины параболы (-1; -4)

2) Область определения и область значения.

D(y) = x ∈ R

E(y) = y ∈ [-4; +∞)

3) Направление ветвей.

Если числовой коэффициент при х² положителен, то ветви напрвлены вверх.

1 > 0 ⇒ ветви вверх.

4) Нули функции.

- точки, в которых график пересекает ось Ох.

⇒ у = 0

x² + 2x - 3 = 0

По теореме Виета:

х₁ = -3; х₂ = 1

5) Промежутки знакопостоянства.

Данный график пересекает ось Ох в точках 1 и (-3).

Определим знаки функции на промежутках:

$+++[-3]---[1]+++$

y > 0 при х ∈ (-∞; -3) ∪ (1; +∞)

y < 0 при х ∈ (-3; 1)

6) Промежутки возрастания и убывания.

х₀ = -1

⇒ функция убывает при х ∈ (-∞; -1]

функция возрастает при х ∈ [-1; +∞)

7) Наибольшее и наименьшее значение функции.

Наименьшее значение функция имеет в точке вершины.

у наим. = -4

Наибольшего значения функция не имеет (+∞)

8) Нарисуйте точный график данной функции.

Найдем дополнительные точки:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| }\cline{1-5}x& -2 & 0 & -4& 2 \\\cline{1-5}y& -3 & -3 & 5& 5 \\\cline{1-5}\end{array}$

Отметим точки на координатной плоскости и построим график.

#SPJ1