Question

Помогите решить, заранее спасибо

Answer 1

касательные, проходящие через начало координат имеют вид

y=kx

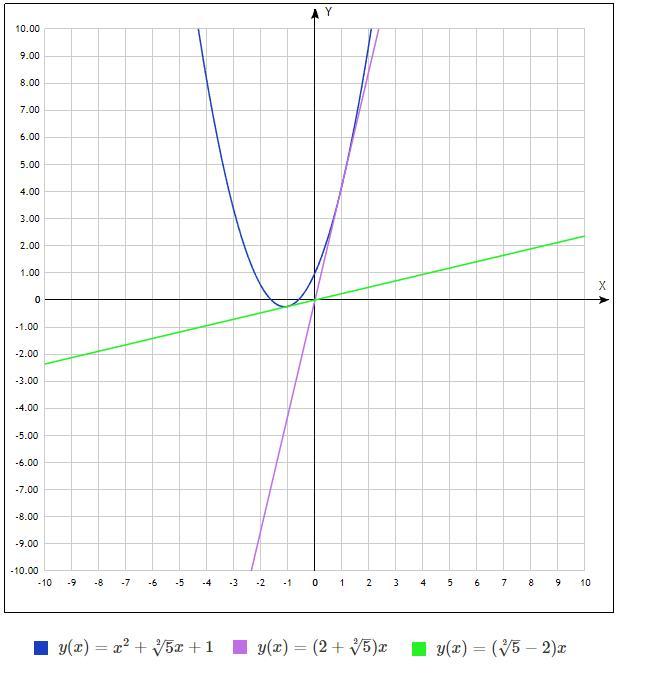
f(x)=x^2+bx+1

k=f`(x)=2x+b

Если точка касания параболы и касательной х0, то

f(x0)=x0^2+b*x0+1

y(x0)=(2x0+b)x0=2x0^2+b*x0

так как эти две функции равны в точке х0, приравняю их правые части

x0^2+bx0+1=2x0^2+b*x0

1=x0^2

x0=1 или -1

k1=k(1)=2*1+b=2+b

k2=k(-1)=b-2

если если тангенс угла между этими касательными равен 2 по условию, то можно вычислить b

tg a=2=(k1-k2)/(1+k1*k2)

2=(2+b-(b-2))/(1+(2+b)(b-2)=4/(1+b^2-4)

b^2-3=4/2

b^2=2+3=5-это ответ

(на рисунке построена парабола и касательные для b=√5)