Предмет: Алгебра,
автор: ludmilakucerova435
Допоможіть будь ласка!!!!!!
Приложения:
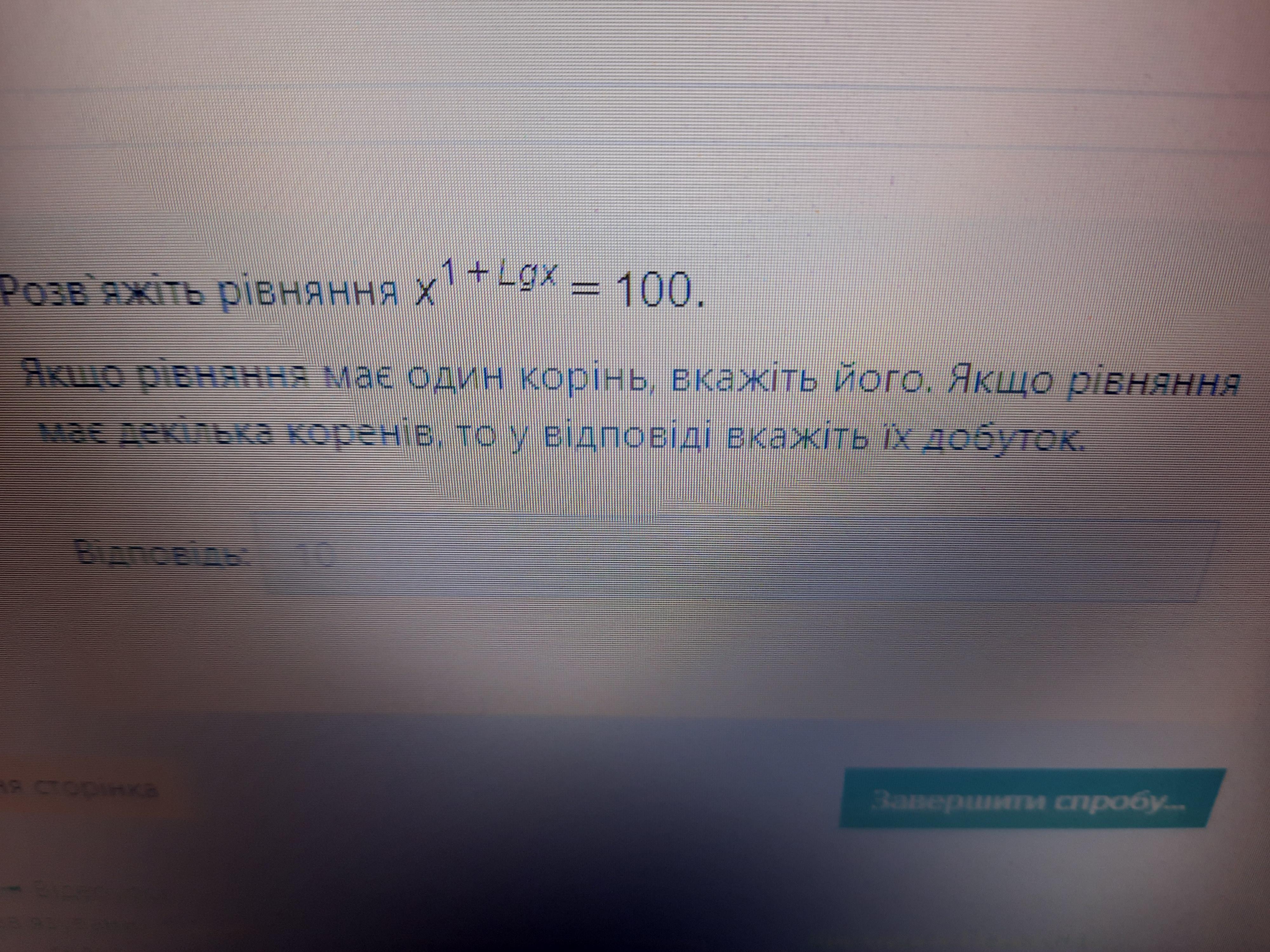
Ответы
Автор ответа:
2
Ответ:
Уравнение имеет два корня: 10, 0,01.
Произведение корней: 10 · 0,01 = 0,1
Объяснение:
Решить уравнение:
Число под знаком логарифма положительно.
⇒ ОДЗ: x > 0;
Прологарифмируем обе части уравнения:
Свойство логарифма:
Выполним замену переменной:
Получим квадратное уравнение и решим его:
Обратная замена:
Уравнение имеет два корня: 10, 0,01.
Произведение корней: 10 · 0,01 = 0,1
Похожие вопросы
Предмет: Физика,
автор: a8038419
Предмет: Математика,
автор: mankovskijvladislav6
Предмет: Английский язык,
автор: ivanunapolina
Предмет: Биология,
автор: slavik200710242141
Предмет: Математика,
автор: uliana3699