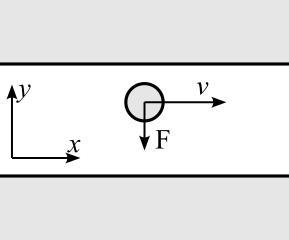
Узкий пучок электронов, обладающих скоростью 20 000 км/с, проходит в вакууме посередине между обкладками плоского конденсатора. Какую наименьшую разность потенциалов нужно при¬ложить к пластинам, чтобы электроны не вышли из конденсатора? Расстояние между пластинами 1 см, длина их 3 см.
Ответы
Ответ:
250 В
Объяснение:
Между обкладками плоского конденсатора возникает однородное электрическое поле E = U / d, где U — разность потенциалов, а d = 0,01 м — расстояние между пластинами. Это электрическое поле при воздействии на заряд q вызывает силу F = qE. Необходимо добиться того, чтобы за время пролёта конденсатора электроны отклонялись от своего начального направления и попадали в обкладки конденсатора.
Запишем уравнения движения одного из электронов.
В проекции на x на электрон не действуют никакие силы, движение в этом направлении равномерное со скоростью v = 2 · 10⁷ м/с; x = vt
В проекции на y на электрон действует постоянная сила со стороны электрического поля. Она приводит к возникновению ускорения a = F / m = qE / m. Уравнение движения: y = -at² / 2.
Если разность потенциалов наименьшая, электрон сталкивается с обкладкой конденсатора в точности в его конце. Значит, по x он пролетит L = 0,03 м за время t = L / v.
За это время он должен отклониться по y на половину расстояния между пластинами d / 2:
aL² / 2v² = d / 2
a = dv² / L²
qE / m = dv² / L²
E = mdv² / qL²
U / d = mdv² / qL²
U = md²v² / qL²
Подставляем в формулу значения d, v, L из условия и значения для электрона — его массу m = 9,1 · 10⁻³¹ кг и заряд q = 1,6 · 10⁻¹⁹ Кл — и получаем U ≈ 250 В.