Question

боковая поверхность правильной четырехугольной призмы имеет площадь 16 дм2.Диагональ основания равна 4 корня из 2.Найдите площадь сечения призмы,проходящего через диагонали двух смежных боковых граней,имеющих общую вершину

Answer 1

в основании правильной четырехугольной призмы лежит квадрат. и она прямая.

значит все боковые грани равны, отсюда S/4 = s1 (s1 - площадь одной грани)

16/4 = 4 = s1

зная диагональ основания найдем ее сторону так как a√2 = d

4√2 = a√2, а = 4

s1 грани равно = а*b = (а сторона основания, b высота призмы)

4 = 4*b, b = 1

найдем диагональ грани по теореме пифагора: х" = 16+1, х = √17

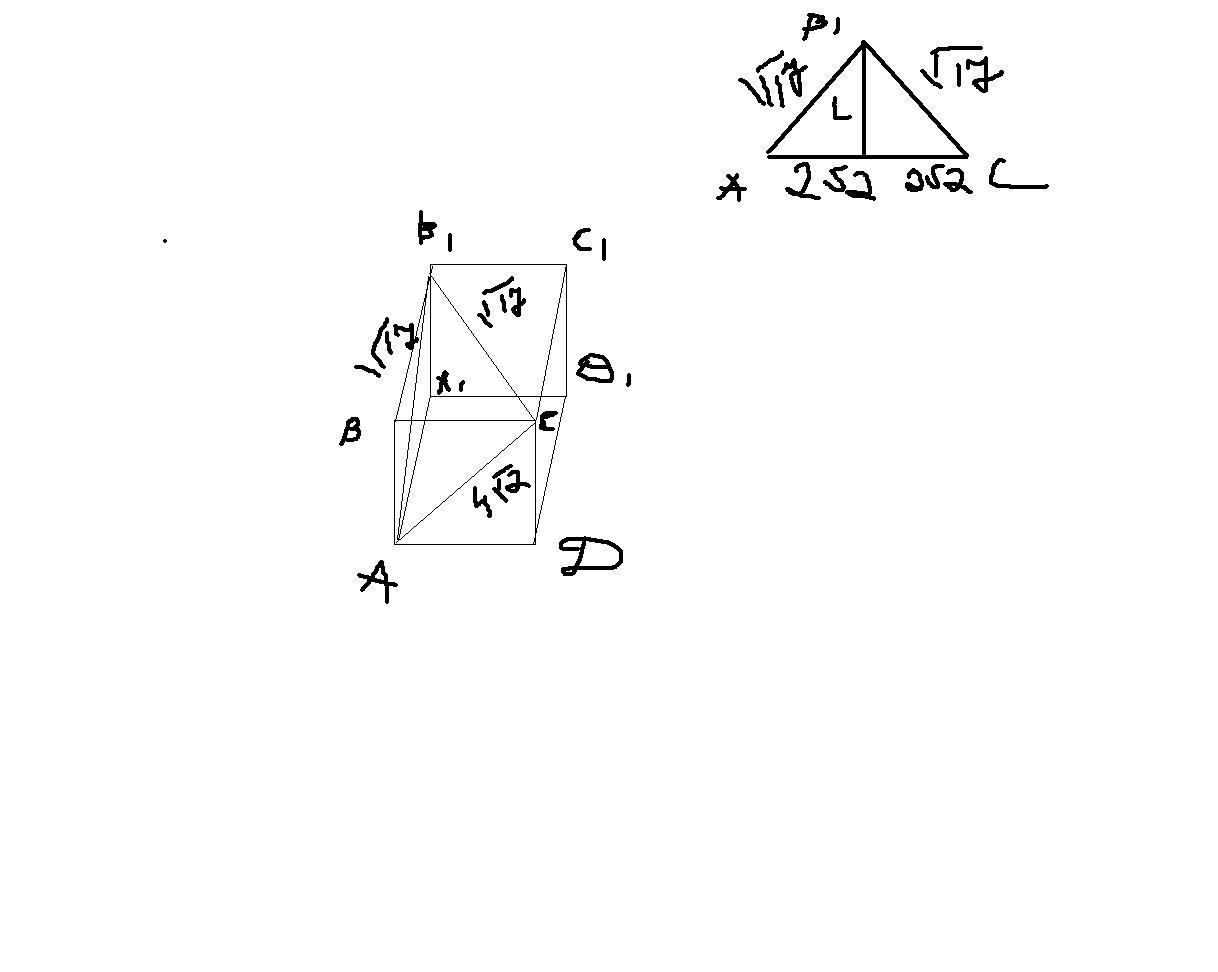
на рисунке видно сечение: АВ1С

из этого треугольника найдем ее высоту L: L" = 17-8 =9

L = √9 = 3

s = h*a*1/2 = 3*4√2*1/2 = 6√2