Предмет: Математика,
автор: Phazed
Помогите решить (ОЧЕНЬ СРОЧНО)
Нужно найти производную функции
Приложения:
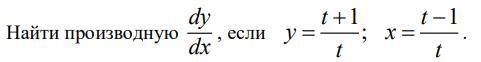
Ответы
Автор ответа:
1
Ответ:
Производная функции, заданной в параметрическом виде. Применяем правило дифференцирования частного :
.
Похожие вопросы
Предмет: Биология,
автор: karolinanaum34
Предмет: Алгебра,
автор: ermekjanel007
Предмет: Английский язык,
автор: katabocek12
Предмет: Русский язык,
автор: pashkove52