Question

Однородный стержень длины l может колебаться в вертикальной плоскости вокруг горизонтальной оси проходящей:
а) через верхний конец стержня
б) на расстоянии b от центра стержня.
Найти отношение частот малых колебаний в двух этих случаях

Answer 1

Ответ:

$\sqrt{\dfrac{l^2+12b^2}{8lb}}$

Объяснение:

Выведем сначала выражение для частоты колебаний физического маятника. Пусть есть некоторое тело, закреплённое на неподвижной оси O, расстояние от которой до центра инерции тела равно a, и отклонённое на угол φ от положения равновесия.

На тело действует момент силы тяжести -mga sin φ, стремящийся вернуть его в положение равновесия. Если момент инерции тело относительно оси O равен J, то можно написать уравнение

$J\ddot\varphi=-mga\sin\varphi\\J\ddot\varphi+mga\sin\varphi=0$

Если угол отклонения мал, то можно заменить синус угла на сам угол, получится уравнение гармонических колебаний

$J\ddot\varphi+mga\varphi=0\\\ddot\varphi+\underbrace{\dfrac{mga}{J}}_{\omega_0^2}\varphi=0$

Найдём отношение квадратов частот.

Известно, что момент инерции однородного стержня массы m и длины l относительно оси, проходящей через его центр, равен ml² / 12. По теореме Штейнера момент инерции стержня относительно оси, сдвинутой на a относительно его центра, равен ml² / 12 + ma².

а) ось проходит через верхний конец стержня

a = l / 2, тогда J = ml² / 3.

ω₁² = mgl/2 : (ml² / 3) = 1.5 g / l

б) ось проходит на расстоянии b от центра

a = b; J = ml² / 12 + mb²

ω₂² = mgb / (ml² / 12 + mb²) = 12gb / (l² + 12b²)

Отношение квадратов частот:

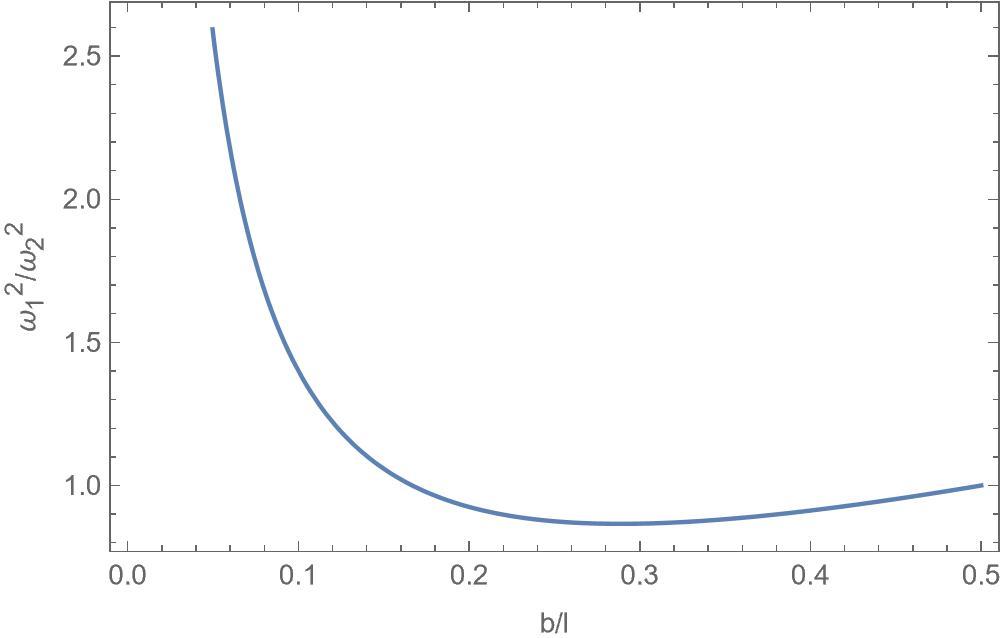
ω₁ : ω₂ = (l² + 12b²) / (8 l b)

Тогда отношение частот будет равно квадратному корню из этого выражения.