Предмет: Математика,
автор: TheSash1
Помогите сделать дз по математике.
Найти производную функции
Приложения:
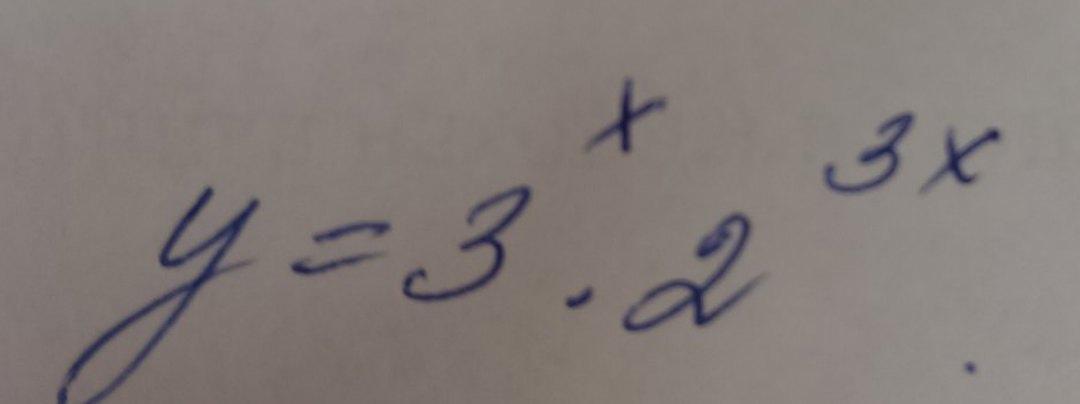
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Найти производную функции:
Формулы:
Найдем производную:
Похожие вопросы
Предмет: Українська мова,
автор: Lohfh
Предмет: Українська мова,
автор: vpirkun
Предмет: География,
автор: 2rndmb7jnh
Предмет: Музыка,
автор: paulkinadaria
Предмет: Алгебра,
автор: yulyagrishko00