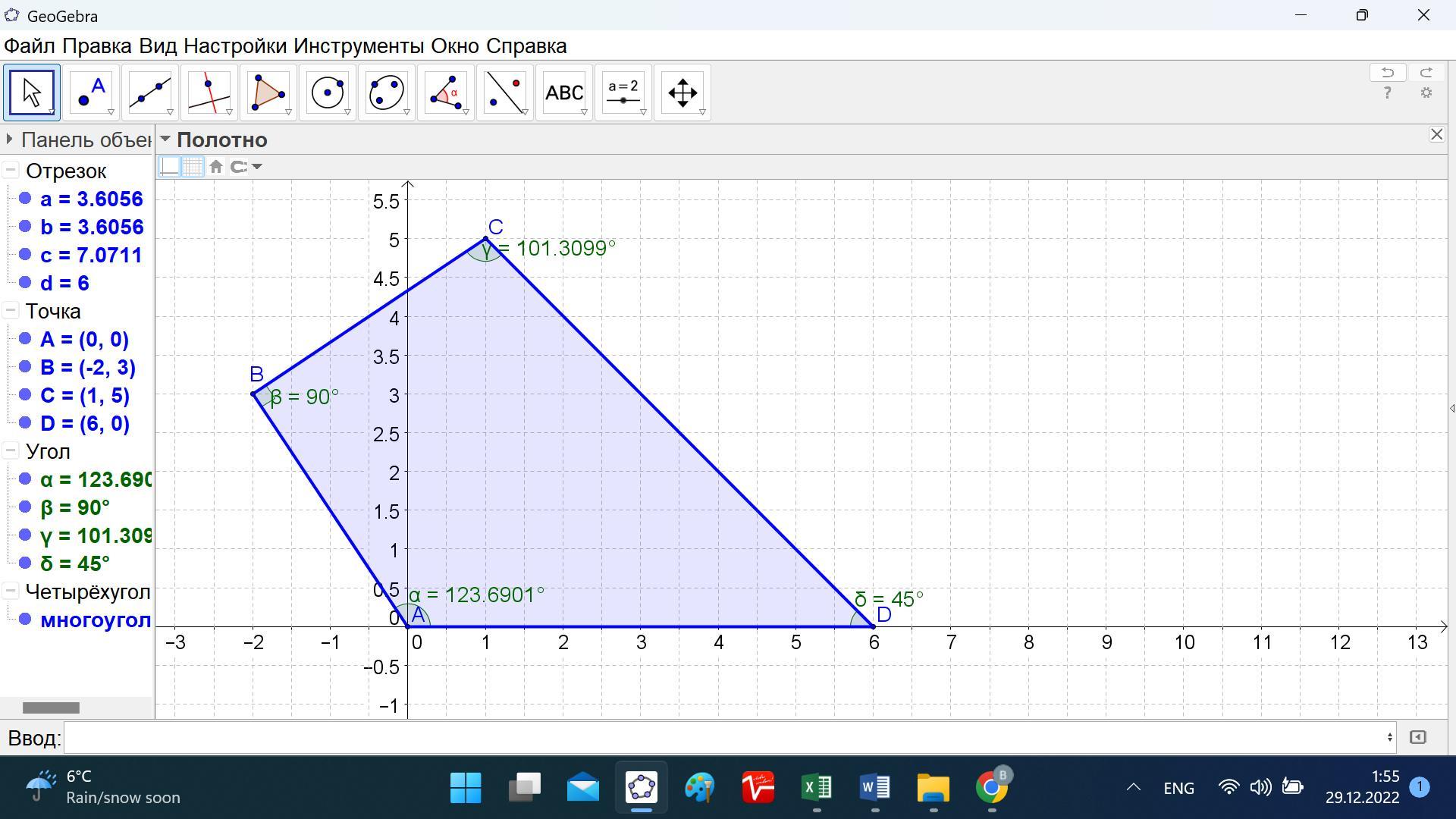
Есть четырехугольник, с координатами A(0 0) B(-2; 3 ) C(1; 5) D(6; 0) O(0.4; 2), определите, можно ли около этого четырехугольника описать окружность
Ответы
Находим углы четырёхугольника ABCD.
Для этого определяем векторы сторон и их модули.
Далее находим углы по формуле:
cos A = (a(x)*b(x) + a(y)*b(y))/(|a|*|b|).
Точка А Точка В Точка С Точка D
х у х у х у х у
0 0 -2 3 1 5 6 0.
Вектор АВ Вектор CD Вектор ВC
x y x y x y
-2 3 5 -5 3 2
3,605551275 7,071067812 3,605551275
Вектор АD Вектор АC Вектор ВD
x y x y x y
6 0 1 5 8 -3
6 5,099019514 8,544003745
cos A = -0,554700196
A = 2,15879893 радиан
123,6900675 градуса.
cos B = 0
B = 1,570796327 радиан
90 градусов.
cos C = -0,196116135
C = 1,768191887 радиан
101,3099325 градуса.
cos D = 0,707106781
D = 0,785398163 радиан
45 градусов.
Как видим условие равенства суммы противоположных углов 180 градусам не выполняется.
Ответ: около заданного четырёхугольника невозможно описать окружность.