Предмет: Математика,
автор: tupovatiy228
Помогите решить уравнение!!
Приложения:
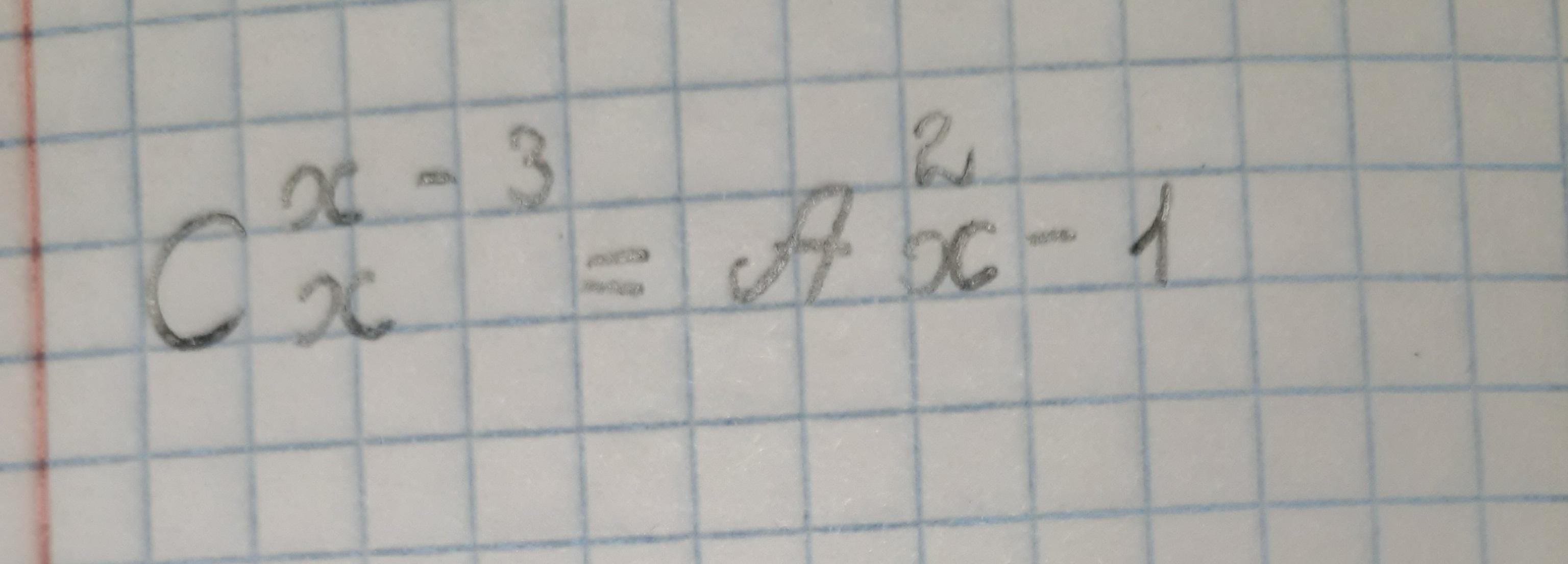
Ответы
Автор ответа:
1
Ответ: x = 6
Пошаговое объяснение:
Формула сочетаний :
Формула размещений :
Теперь перейдем к решению :
Учтем ОДЗ :
Воспользуемся свойством факториала :
Из чего исходя :
#SPJ1
Похожие вопросы
Предмет: Математика,
автор: aakirill16
Предмет: Другие предметы,
автор: timapetrenko16
Предмет: Математика,
автор: jarikpakhomz
Предмет: Русский язык,
автор: dinaa462
Предмет: Математика,
автор: nikaniaf24