Question

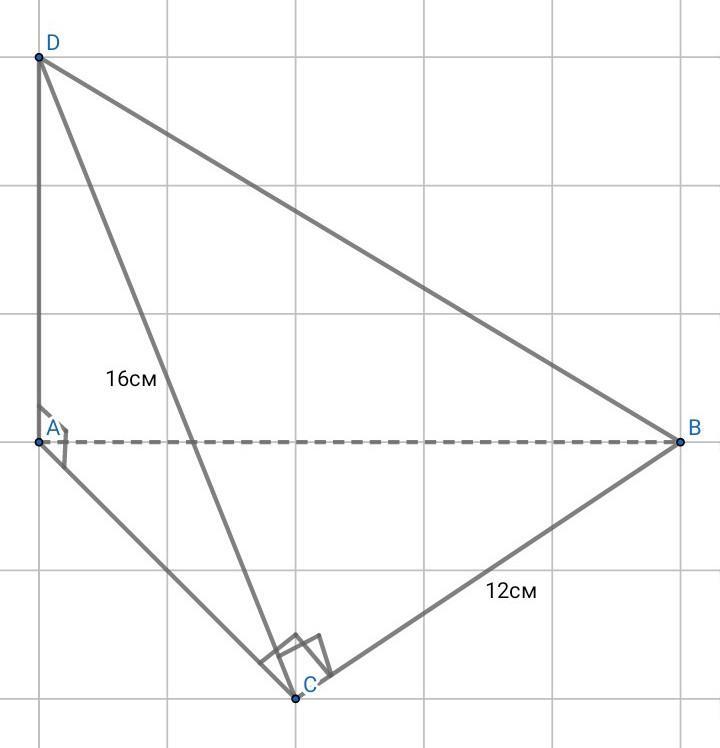
через вершину A прямоугольного треугольника ABC с прямым углом C проведена прямая AD перпендикулярная плоскости треугольника
a) Докажите что треугольник CBD прямоугольный
b) Найдите BD если BC = 12 см , DC = 16 см​

Answer 1

Ответ:

a) см.объяснение

b) BD = 20см

Объяснение:

Дано: ∆АВС - прямоугольный , ∠АСВ = 90°, AD⊥(ABC).

a) Доказать , что ∆СВD - прямоугольный

b) BC = 12см , DC = 16см , Найти BD

Доказательство:

Так как DC - наклонная , а АС - проекция наклонной DC на (АВС) и BC⊥AC , то по теореме о трёх перпендикулярах BC⊥DC , следовательно , ∆СВD - прямоугольный.

Решение:

Рассмотрим прямоугольный ∆CBD , по т.Пифагора:

$DC^2+BC^2=BD^2 \\ 16 {}^{2} + 12 {}^{2} = BD^2 \\ BD = \sqrt{16 {}^{2} + 12 {}^{2} } = \sqrt{256 + 144 } = \sqrt{400} = 20$

Ответ: BD = 20(см)