Question

решения не нужно, просто отправьте чертеж​

Answer 1

Ответ:

АВ=CD=20 см

AD=BC=40 см

Объяснение:

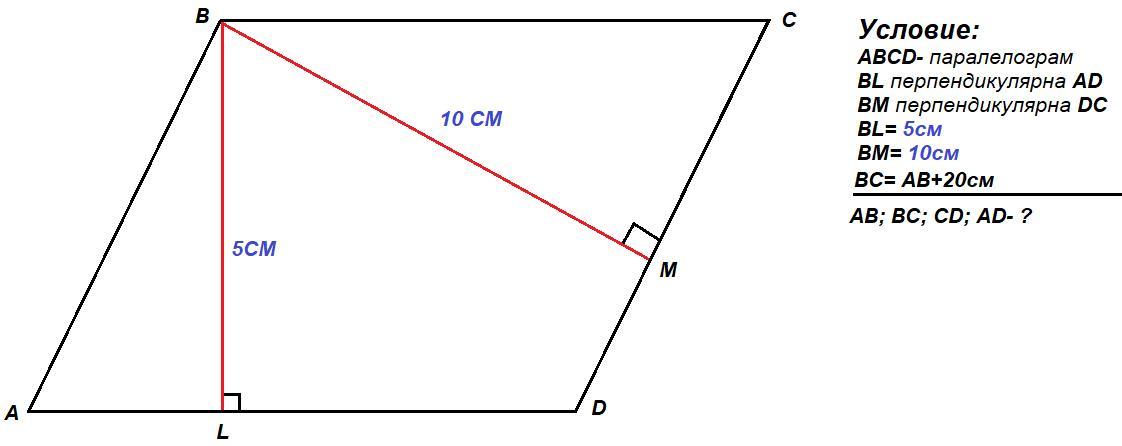
!Условие задачи и рисунок к ней закреплены с низу.

Будем постепенно рассматривать рисунок и решать задачу.

1. Начнем с того что мы знаем по условию и чем это может помочь.

По условию есть две высоты   BL и BM которые равны 5см и 10см.

Так же мы знаем что одна из сторон параллелограмма больше чем другая на 20см. То есть  сели мы возьмём сторону AB за х,  то у нас выйдет ВС=х+20. Так же не стоит забывать, что AB=CD; BC=AD так как АВСD параллелограмм. Зная эти все данные что мы можем с ними сделать?  С помощью этих данных мы можем выразит площадь параллелограмма.

Формула площади параллелограмма:  $S=a*h_{a}$

Где а-сторона параллелограмма, а ha-высота опущенная на сторону а.

Зная это мы можем два раза выразит площадь параллелограмма, так как у нас есть две разные высоты опущенные на две разные стороны.

Но стоит помнить что площадь будет одна и таже, соответственно то что мы выразим приравняем между собой и получим уравнение.

$S=BL* AD\\S=5*(x+20)$              $S=BM*CD\\S=10x$

                   ↓

                 $S=S\\BL*AD=BM*CD\\5*(x+20)=10x$

Зная это теперь решим уравнение и найдём стороны АВ и CD так как они равны х.

$5*(x+20)=10x\\5x+100=10x\\100=5x\\x=20$

↓

АВ=CD=20 см

↓

AD=BC=x+20

↓    

AD=BC=40 см    

Вот мы и нашли все что требовалось в задаче.