Question

исследуйте функцию у=2х^2 +4х+9 на экстримумы помогите пожалуйста ​

Answer 1

Ответ:

x=-1 - минимум,

Функция возрастает на промежутке: [-1;∞)

Функция убывает на промежутке (-∞;-1]

Пошаговое объяснение:

Экстремумы это точки в которых производная функции равна 0 и при прохождении через которые производная меняет знак. Вычислим производную:

$y' = 4x+4 = 4(x+1)\\4(x+1) = 0\\x = -1$

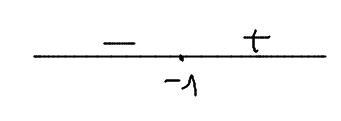
У функции есть одна критическая точка: -1. Определим знак производной слева и справа от -1, чтобы понять тип экстремума, то есть минимум это или максимум (см. рисунок).

По рисунку видно, что функция убывает до -1 и затем начинает возрастать. Следовательно:

-1 это минимум.

Функция убывает на промежутке (-∞;-1]

Функция возрастает на промежутке: [-1;∞)