СРОЧНО 40 БАЛЛОВ
РЕШИТЕ ХОТЯ БЫ ОДИН
Решите неравенство
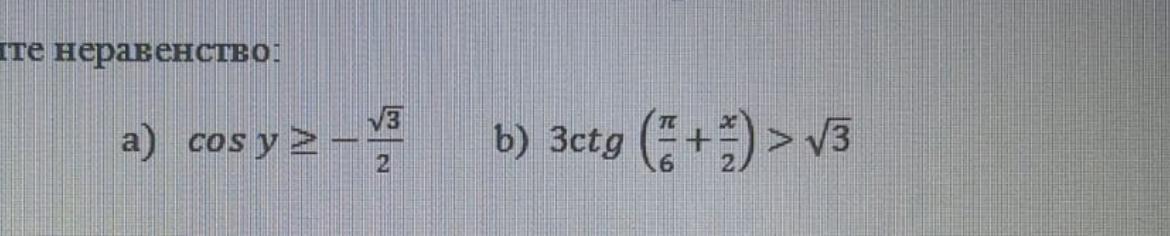
Ответы
Ответ:
-1/sqrt3 >= (cos(y) - 1)^2 или y ∈ ℝ.
Объяснение:
а) cos y / cos y >= -sqrt3/2 / cos y | Первым действием поделим на косинус
Следовательно, неравенство принимает вид:
1 >= -sqrt3/2cos(y)
Чтобы решить это неравенство, мы можем умножить обе части на -2/sqrt3, чтобы получить:
-2/sqrt3 >= -cos(y)
Затем мы можем добавить 1 к обеим сторонам, чтобы получить:
-2/sqrt3 + 1 >= -cos(y) + 1
Упрощение левой части дает нам:
-1/sqrt3 >= 1 - cos(y)
Наконец, мы можем переставить члены в правой части, чтобы получить:
-1/sqrt3 >= cos^2(y) - cos(y) + 1
Это упрощается:
-1/sqrt3 >= (cos(y) - 1)^2
Это неравенство всегда верно, потому что правая часть представляет собой квадрат действительного числа и, следовательно, неотрицательна. Следовательно, решение исходного неравенства y принадлежит множеству всех действительных чисел.
Мы также можем записать это решение как y ∈ ℝ.