Предмет: Математика,
автор: xxxlora
Помогите решить интеграл
Приложения:
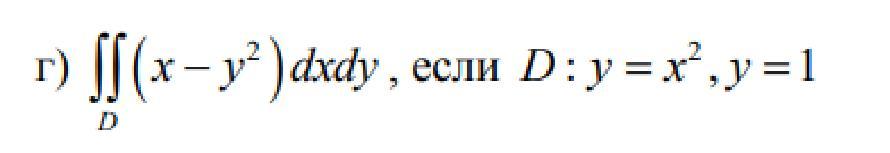
Ответы
Автор ответа:
1
Ответ:
Двойной интеграл вычислить .
Область .
Точки пересечения: .
Похожие вопросы
Предмет: Литература,
автор: nastyaprohorova4596
Предмет: Английский язык,
автор: platonuvucovic
Предмет: Информатика,
автор: cebureky123
Предмет: Математика,
автор: Danilhpr
Предмет: Русский язык,
автор: Аноним