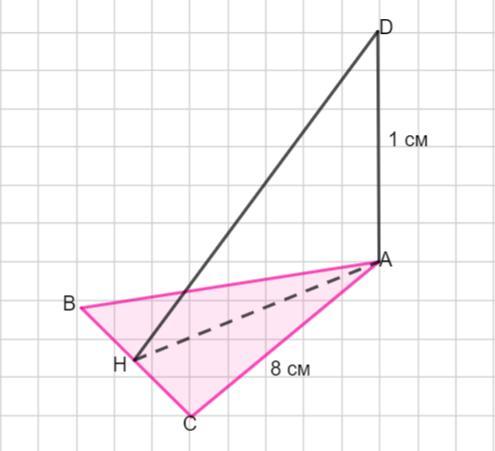
Отрезок AD перпендикулярен к плоскости равносторонего треугольника ABC.известно что BC=8 см AD=1 см.найдите расстояние от концов отрезка AD до прямой BC
Ответы
Ответ:
Расстояние от точки А до прямой ВС равно 4√3 см, а расстояние от точки D до прямой ВС равно 7 см.
Объяснение:
Отрезок АD перпендикулярен к плоскости равностороннего треугольника АВС . Известно, что ВС =8 см , АD = 1 см. Найти расстояние от концов отрезка АD до прямой ВС.
Пусть дан Δ АВС равносторонний. АВ =ВС =АС = 8 см. К плоскости треугольника проведен перпендикуляр АD = 1 см.
Расстояние от точки А до прямой ВС будет высота АН равностороннего треугольника.
Высота равностороннего треугольника определяется по формуле
, где а - сторона треугольника.
Тогда см.
Так как АН ⊥ ВС , то по теореме о трех перпендикулярах DН ⊥ВС и длина DН является расстоянием от точки D до прямой ВС.
Рассмотрим ΔDАН - прямоугольный.
По теореме Пифагора : в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
cм
#SPJ1