Предмет: Алгебра,
автор: rain0313
Номер 39.35
Помогите, решите под всеми буквами)
Заранее большое спасибо)
Приложения:
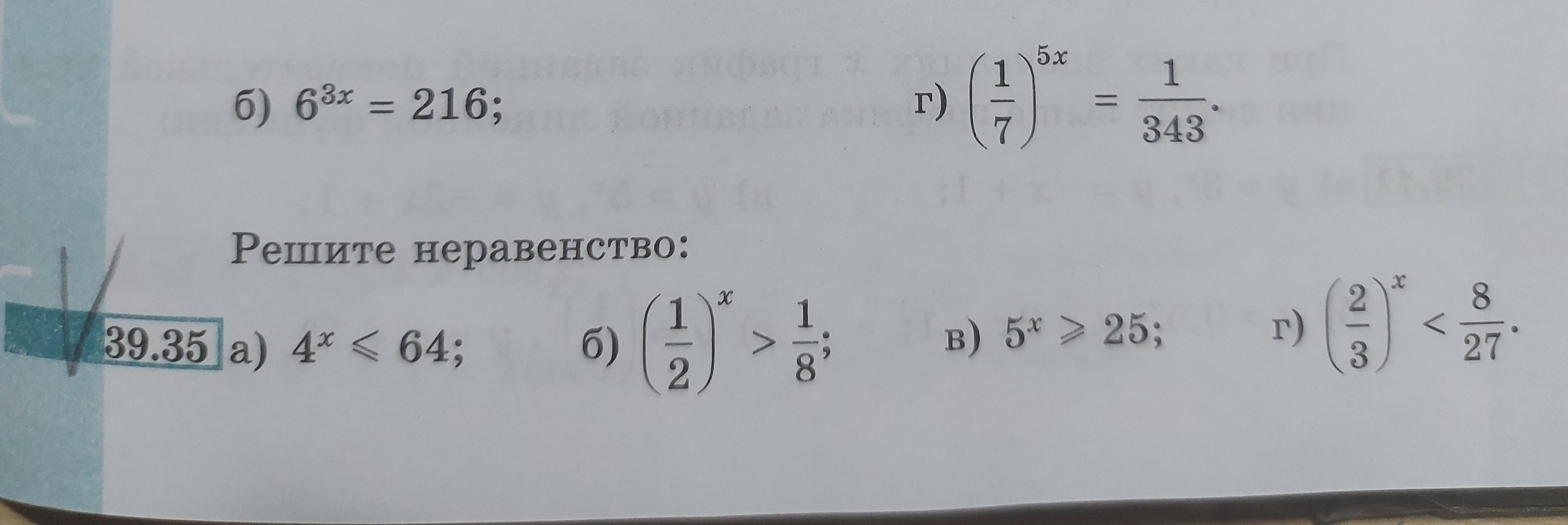
Ответы
Автор ответа:
3
Ответ:
Показательные неравенства.
Так как функция возрастающая функция, то между показателями степеней сохранится тот же знак, что и между функциями, поэтому
Так как функция убывающая функция, то между показателями степеней надо записать знак, противоположный тому знаку, что стоит между функциями, поэтому
Аналогично решаем остальные примеры .
Автор ответа:
1
Ответ:
см.объяснение
Объяснение:
Так как 0<1/2<1 то знак неравенства меняется на противоположный.
Так как 0<2/3<1 то знак неравенства меняется на противоположный.
Похожие вопросы
Предмет: История,
автор: valiama
Предмет: Информатика,
автор: vezelvul94
Предмет: Экономика,
автор: terziolesya40
Предмет: Русский язык,
автор: bermetOsmonkulova
Предмет: Русский язык,
автор: irpila08