Question

треугольник ABC и MPO равны. BC=35 см,угол A=65 градусов,угол C=102 градуса. найдите соответствующие углы и стороны треугольника MPO.​

Answer 1

Объяснение:

Дано:

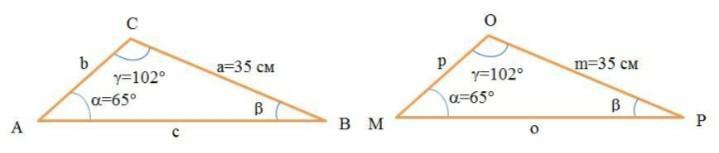
ДАВС = ДМРО (см. рисунок)

BC=35 CM

<A=65°

<C=102°

Найти: МР, РО, MO, za, <B, ZY.

Решение. Сумма внутренних углов

треугольника равна 180°, поэтому в треугольнике АВС:

<A+<B+<С=180°.

Так как <A=65° и <С=102°, то <B=180°-ZA-<С=180°-65°-102°=13°.

Так как треугольники АВС и МРО равны, то соответствующие углы также равны:

<a=<A=<M=65°, <B=<B=<P=13°, <ү=<C=2O=102°.

Далее, по теореме синусов:

BC/sin<A=AC/sin<B=AB/sin<C

Подставим известные значения:

35/sin65°=AC/sin13°=AB/sin102°

Отсюда:

AC=35×sin13°/sin65°≈35×0,22495105/0,90630779≈8,6872107212054

АВ= 35×sin102°/sin65°≈35×0,9781476/0,90630779≈37,774326092904

Так как треугольники АВС и МРО равны, то соответствующие стороны также равны:

a=BC=PO=35 СМ; b=АС=МО=8,69 СМ; C=AB=MP-37,77 CM.