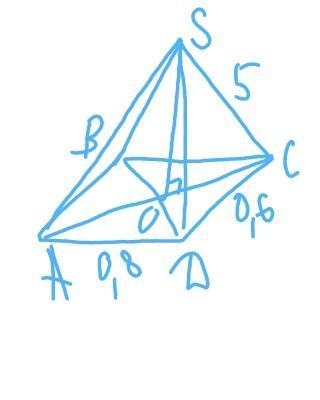ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО

Ответы
Ответ:
КО=1,5√11 (дм)
Объяснение:
ЗАДАЧА:
Основанием пирамиды является прямоугольник, его стороны равны 0,6 дм и 0,8 дм. Каждое боковое ребро равно 5 дм. Найдите высоту пирамиды.
ДАНО:
КАВСД – пирамида; АД=0,8 дм; СД=0,6 дм, АК=ВК=СК=ДК=5 дм
НАЙТИ: высоту пирамиды
РЕШЕНИЕ: проведём диагонали прямоугольника – АС и ВД, точкой их пересечения обозначим точку О. Так как все рёбра пирамиды равны, то основание высоты приходится на точку О, искомая высота пирамиды – КО. Одна диагональ делит прямоугольник на 2 равных прямоугольных треугольника АВС и АДС. Рассмотрим ∆АДС, в нём АД и СД – катеты, а АС – гипотенуза. Найдём АС по теореме Пифагора:
АС²=АД²+СД²= (0,8)²+(0,6)²=0,64+0,36=1.
АС=√1=1 (дм). Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому
АО=СО=1÷2=0,5(дм).
Рассмотрим ∆КСО, он прямоугольный, КО и СО – катеты, а КС – гипотенуза. Найдём искомую высоту КО по теореме Пифагора:
КС²=КО²+СО² → КО²=КС²–СО²=5²–(0,5)²=25–0,25=24,75
КО=√24,75=√(1,5•1,5•11)=1,5√11 (дм)

Объяснение:
SABCD - пирамида
АВ=СD=0,6 дм
ВС=АD=0,8 дм
SA=SB=SC=SD=5 дм
найти: SO
∆АВС - прямоугольный:
по теореме Пифагора:
АС=√(АВ²+ВС²)=√(0,6²+0,8²)=√1=1 дм.
Диагонали ACи ВDпрямоугольника ACВD равны и точкой пересечения O делятся пополам:
ОС=АС:2=1:2=0,5 дм
∆SOC - прямоугольный:
по теореме Пифагора:
SO=√(SC²-OC²)=√(5²-0,5²)=√24,75=
=√2475/100=(15√11)/10=3/2•√11 дм
ответ: 3/2•√11 дм