Предмет: Алгебра,
автор: daniakucher292
Обчисліть площу фігури, обмеженої лініями Будь ласка . даю 50 балів
Приложения:
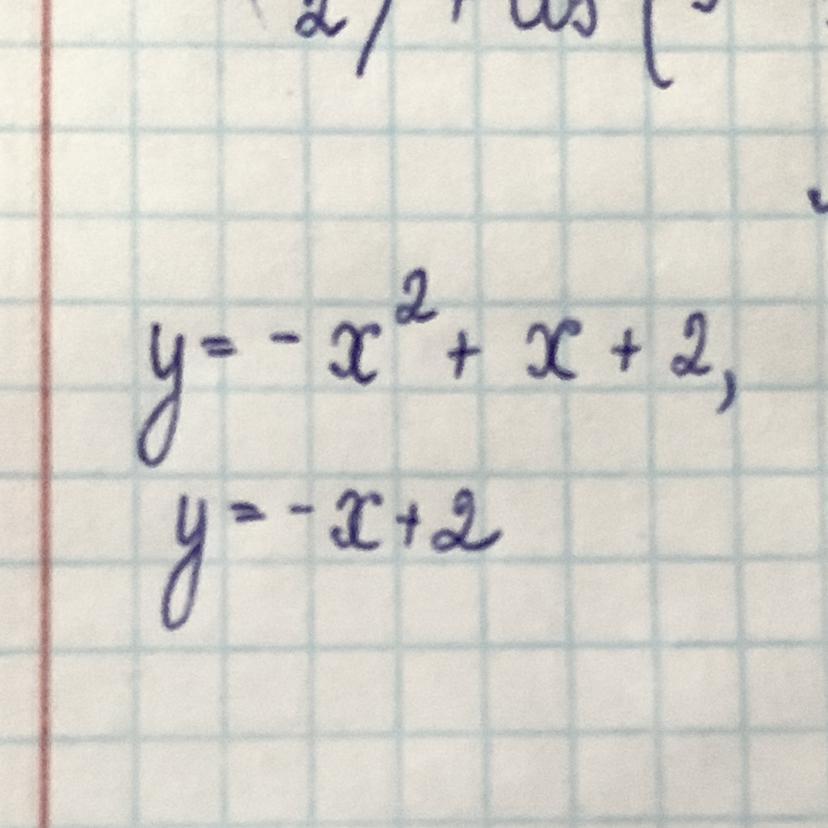
Ответы
Автор ответа:
1
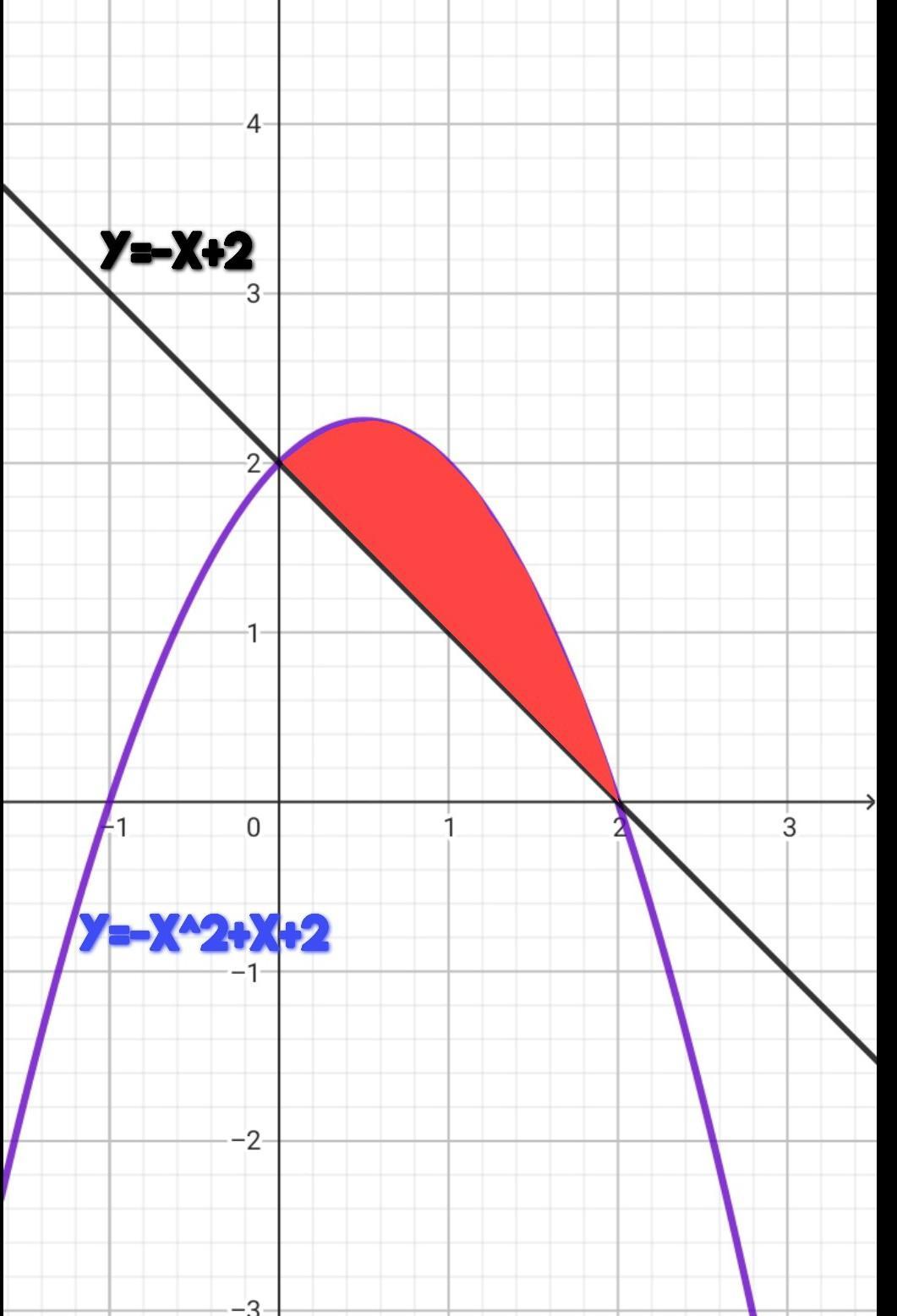
y = -x² + x + 2 – парабола, с ветвями, направленными вниз(а<0) и с вершиной в точках (0,5; 2,25).
у = -х + 2 — прямая, сдвинутая на +2 вдоль оси ординат.
Найдем пересечение:
Область, закрашенная красным оттенком – искомая.
Введем интегрирование:
Приложения:
daniakucher292:
Дуже дякую)
радий допомогти
Похожие вопросы
Предмет: Математика,
автор: uliagorodinska
Предмет: Химия,
автор: ania1518
Предмет: Українська мова,
автор: romanukpro228
Предмет: Математика,
автор: Liie
Предмет: Қазақ тiлi,
автор: naruuuto666