Question

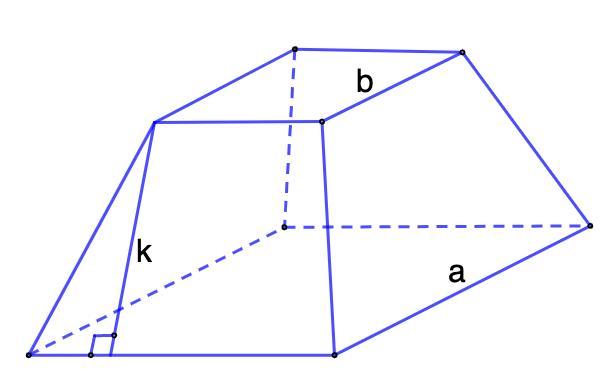
1. В правильной усечённой четырёхугольной пирамиде стороны основания равны а и b, а апофема равна k. Найдите плошадь боковой поверхности усечённой пирамиды. A) S=0,5(a+ b) B)S=1,5(a+b)k C)S=2(a+b)k D)S=(a+b)k.

Answer 1

Ответ:

C)  S = 2 (a + b) k

Объяснение:

1. В правильной усечённой четырёхугольной пирамиде стороны основания равны а и b, а апофема равна k. Найдите плошадь боковой поверхности усечённой пирамиды.  

A) S=0,5(a+ b);  B) S=1,5(a+b)k; C) S=2(a+b)k; D) S=(a+b)k.

Дано: правильная усеченная пирамида;

Стороны основания а и b, апофема - k.

Найти: S бок.

Решение:

Площадь боковой поверхности правильной усеченной пирамиды:

        S бок. = 1/2 (Р₁ + Р₂) · l,

где Р₁ и Р₂ - периметр оснований, l - апофема.

• В правильной усеченной пирамиде в основаниях лежат квадраты.

⇒ Р₁ = 4a; P₂ = 4b.

Апофема l = k.

Подставим данные в формулу:

S бок. = 1/2 · (4a + 4b) · k = 1/2 · 4 ·(a + b) · k =

= 2 (a + b) k

Ответ: C)  S = 2 (a + b) k

#SPJ1