Предмет: Геометрия,
автор: moysig
Срочно. С подробным решением. Задание на фото
Приложения:

Ответы
Автор ответа:
1
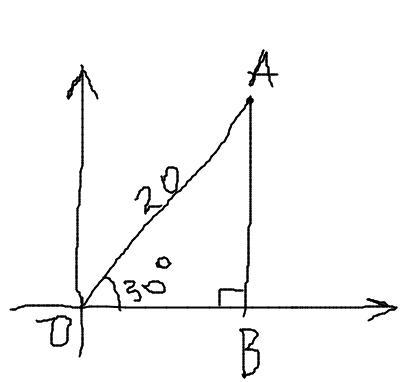
Дано: OA = 20, ∠α=30°
Найти: x, y
Решение:
Опустим перпендикуляр из точки A на ось x в точку B.
Δ AOB прямоугольный: OA - гипотенуза, OB и AB - катеты.
Соответственно x=OB, y=AB.
По определению, синус угла это отношение противолежащего к нему катета к гипотенузе, а косинус угла, это отношение прилежащего к нему катета к гипотенузе. Следовательно:
В итоге:
Ответ:
Приложения:
moysig:
Спасибо
Похожие вопросы
Предмет: Литература,
автор: carparking7850821
Предмет: Литература,
автор: antalowcikaroline
Предмет: Математика,
автор: utkinamilana925
Предмет: Информатика,
автор: zereaikyn
Предмет: Физика,
автор: kasymbekhalima