пмгите пж
оч нужн нуждс ввас
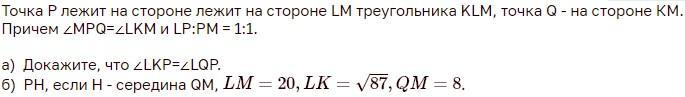
Ответы
Ответ:
a) Чтобы доказать, что угол LKP равен углу LOP, мы можем использовать теорему о среднем перпендикуляре.
Согласно теореме, если точка лежит на прямой, то перпендикуляры, проведенные из этой точки на две разные прямые, делят эти прямые пропорционально.
Таким образом, мы можем применить эту теорему к треугольнику LKP. Точка P лежит на стороне LM, а точка O лежит на стороне KM. Поэтому мы можем провести перпендикуляры из точки L на эти две прямые.
Обозначим эти перпендикуляры LP и LO соответственно. Также, обозначим расстояние от точки L до точки P через x, а расстояние от точки L до точки O через y.
Так как угол LKP равен уголу LOP, то углы LKP и LOP соответственно равны 90 градусам. Поэтому углы LPK и LPO соответственно равны 90 - угол LKP.
2) Сначала найдем расстояние от точки Р до точки К. Так как угол <LKM равен углу <MPQ, то мы можем использовать теорему о равных противоположных углах в треугольнике. По этой теореме стороны, соединяющие центры углов треугольника, равны. Таким образом, PK = LK.
Также мы знаем, что LP:PM = 1:1, то есть LP = PM. Отсюда мы можем выразить расстояние PK через расстояние PM: PK = LP + PM = 2 * PM.
Теперь найдем расстояние PM. Так как точка М - середина стороны QM, то мы можем выразить расстояние PM через расстояние QM: PM = QM / 2 = 8 / 2 = 4.
Теперь мы можем выразить PK через PM: PK = 2 * PM = 2 * 4 = 8.
Таким образом, расстояние РН равно PK - LK = 8 - √87 = 8 - 3√7 = 5√7 - 3√7 = 2√7.
Ответ: РН = 2√7.