Предмет: Математика,
автор: brawlstars92v
Помогите срочно с решением,дам 50 баллов
Приложения:
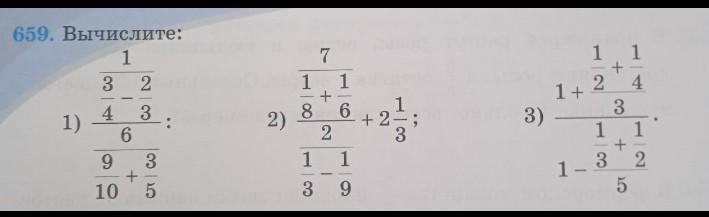
Ответы
Автор ответа:
1
Ответ:
Вычислить . Выполняем действия с дробями. Применяем правило:
.
brawlstars92v:
спасибо
пожалуйста
Похожие вопросы
Предмет: Алгебра,
автор: alinamakao73
Предмет: Українська мова,
автор: Biuedy
Предмет: Алгебра,
автор: 4zcm6tvd2x
Предмет: Русский язык,
автор: VoutBoy165
Предмет: Другие предметы,
автор: karunamarkovets