Question

ВАРИАНТ 2 СРОЧНО !!!!!!!!​

Answer 1

Ответ:

Периметр трапеции равен 28 см.

Средняя линия трапеция равна 8 см.

Объяснение:

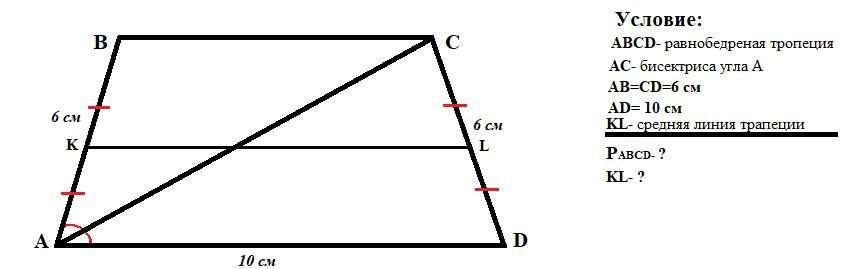
В равнобедренной трапеции диагональ является биссектрисой острого угла. Вычислите периметр трапеции и ее среднюю линию, если ее большая основа и боковая сторона равны соответственно: 10 см и 6 см.

Дано: ABCD - равнобедренная трапеция;

АС - диагональ, биссектриса;

AD = 10 см; АВ = СD = 6 см;

Найти: Р(ABCD); MК - среднюю линию.

Решение:

Обозначим углы цифрами (см.рис)

Рассмотрим ΔАВС.

∠1 = ∠2 (АС - биссектриса)

∠3 = ∠2 (накрест лежащие при BC || AD и секущей АС)

⇒ ∠1 = ∠3

• Если в треугольнике равны два угла, то этот треугольник равнобедренный.

⇒ АВ = ВС = 6 см.

• Периметр - сумма длин всех сторон.

Р(ABCD) = AB + BC + CD + AD = 6 + 6 + 6 + 10 = 28 (см)

Периметр трапеции равен 28 см.

• Средняя линия равна полусумме оснований.

МК = (BC + AD) : 2 = (6 + 10) : 2 = 8 (см)

Средняя линия трапеция равна 8 см.

Answer 2

Ответ:

$P_{ABCD} =28cm\\\\KL= 8cm$

Объяснение:

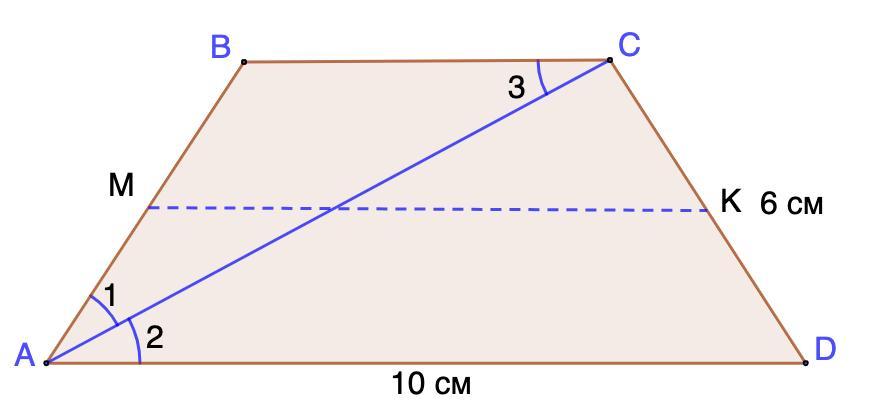
!Условие задачи прикреплено на рисунке в низу ↓

Рассмотрим внимательно рисунок и поэтапно будем решать задачу:

1. Рассмотрим ΔАВС, он является равнобедренным с основой АС. Теперь разберем почему так. Так как АС биссектриса ∠А за условием задачи → ∠ВАС=∠САD. Так как АBCD трапеция, а BC и AD основы → BC ║AD. Зная это мы можем сказать, что  АС- секущая линия → ∠ВСА=∠САD как внутреннее разносторонние углы. Вот мы разобрали почему ΔАВС равнобедренный  с основой АС → AB=BC= 6 см.

2. Мы нашли меньшее основание  трапеции, теперь мы знаем все стороны трапеции → мы теперь можем найти периметр трапеции.

!Напомню что периметр это сума длины всех сторон.

↓

$P_{ABCD} =AB+BC+CD+DA\\P_{ABCD} = 6+6+6+10\\P_{ABCD}=28 cm$

3. Первый этап задачи решен, теперь перейдем ко второму. Найдем среднюю линию трапеции (KL). Как же ее найти ? Средняя линия трапеции равна полу суме ее основ.

↓

$KL=\frac{BC+AD}{2} \\\\KL=\frac{6+10}{2} \\\\KL=8 cm$

Вот мы и нашли все что нужно было.