Предмет: Геометрия,
автор: Аноним
AB и CD − диаметры окружности,
пересекающиеся в точке 0. Докажите, что ∠ABC = ∠CDA.
Ответы
Автор ответа:
1
Ответ:
∠АВС =∠СDА, как вписанные углы , опирающиеся на одну дугу.
Объяснение:
АВ и СD - диаметры окружности, пересекающие в точке О. Доказать, что ∠АВС =∠СDА.
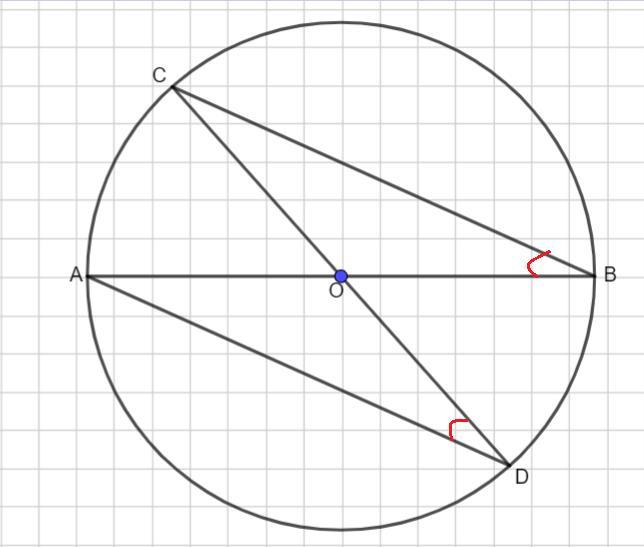
Рассмотрим рисунок. В окружности проведены два диаметра АВ и СD, которые пересекаются в точке О. ∠АВС - вписанный угол, опирающий на дугу АС и ∠СDА - вписанный угол , опирающийся на туже дугу АС.
А вписанные углы, опирающиеся на одну дугу, равны.
Значит, ∠АВС =∠СDА.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: karzaunurik
Предмет: Химия,
автор: 0680461030r
Предмет: Українська мова,
автор: Karlick007
Предмет: Українська мова,
автор: dartveyder2089
Предмет: Математика,
автор: fedorovichveronika20