Question

Помогите пожалуйста очень вас прошу, даю 30 баллов

Answer 1

Ответ:

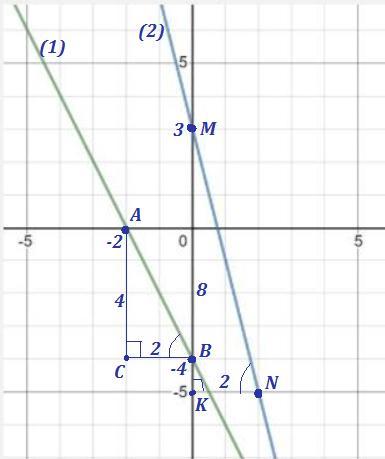
Уравнение прямой имеет вид   $\bf y=kx+b$  , где  k - угловой коэффициент , b - ордината точки пересечения прямой с осью ОУ .

Для прямой  (1)  угловой коэффициент находим из прямоугольного

ΔАВС :  $\bf k=-\dfrac{4}{2}=-2$  ,   $\bf b=-4$  . Тогда уравнение этой прямой имеет

вид    $\bf y=-2x-4$  .

Для прямой  (2)  угловой коэффициент находим из прямоугольного

ΔMNK :  $\bf k=-\dfrac{8}{2}=-4$  ,   $\bf b=3$  . Тогда уравнение этой прямой имеет

вид    $\bf y=-4x+3$  .

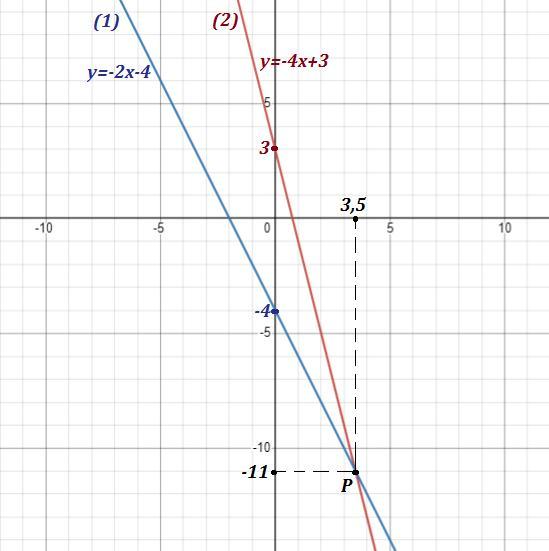
Найдём точку пересечения прямых (1) и (2) :

$\left\{\begin{array}{l}\bf y=-2x-4\\\bf y=-4x+3\end{array}\right\ \ \left\{\begin{array}{l}\bf -2x-4=-4x+3\\\bf y=-4x+3\end{array}\right\ \ \left\{\begin{array}{l}\bf 2x=7\\\bf y=-4x+3\end{array}\right\\\\\\\left\{\begin{array}{l}\bf x=3,5\\\bf y=-4\cdot 3,5+3\end{array}\right\ \ \left\{\begin{array}{l}\bf x=3,5\\\bf y=-11\end{array}\right\ \ \ \Rightarrow \ \ \ \bf P(\ 3,5\ ;\ -11\ )$  

Точка пересечения   $\bf P(\ 3,5\ ;\ -11\ )$   .