Question

ДАЮ 100 БАЛІВ!
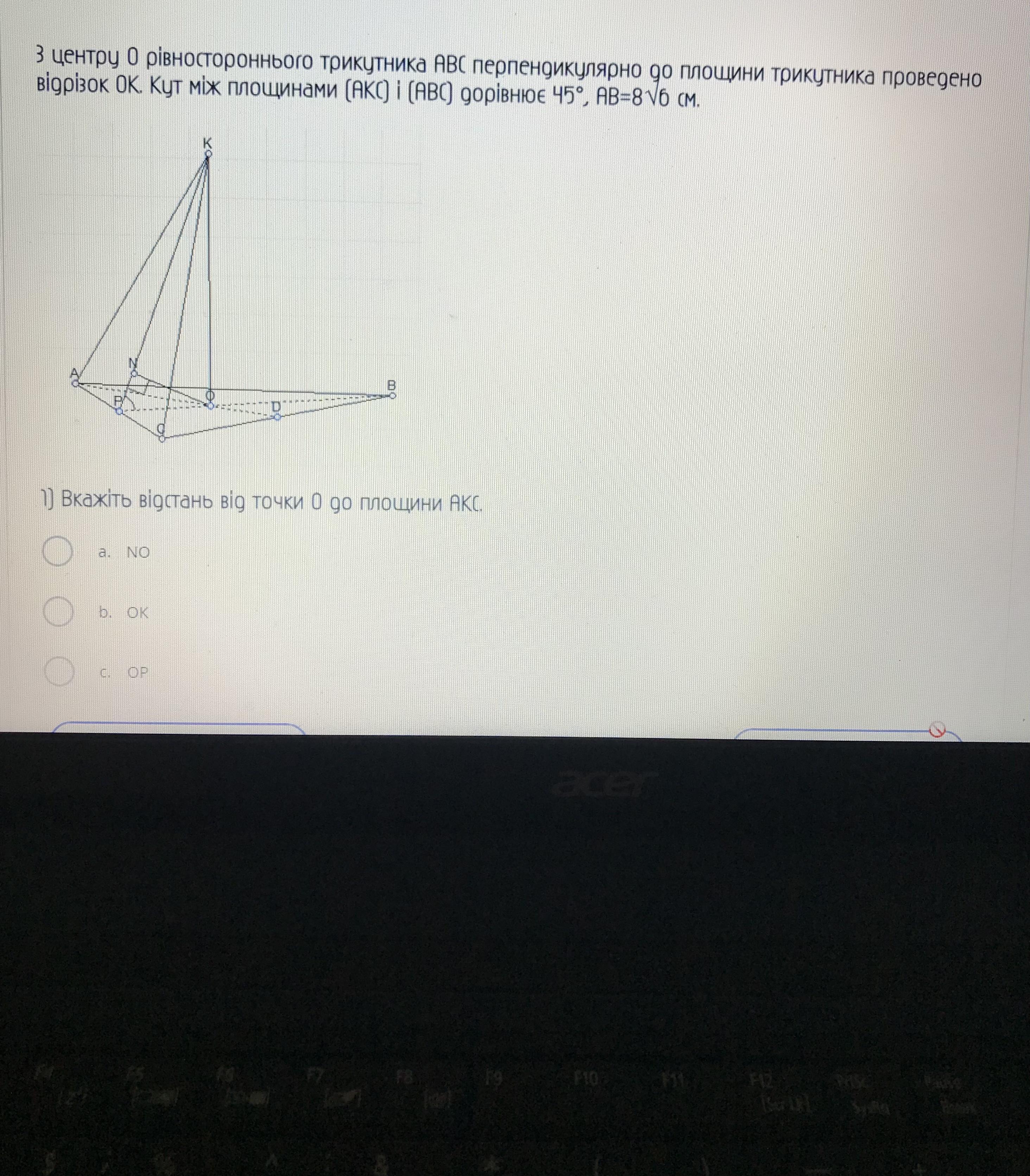
З центру О рівностороннього трикутника ABC перпендикулярно до площини трикутника проведено відрізок ОК. Кут між площинами дорівнює 45 градусів, АВ = 8 корінь з 6.
1) Вкажіть відстань від точки О до площини АКС
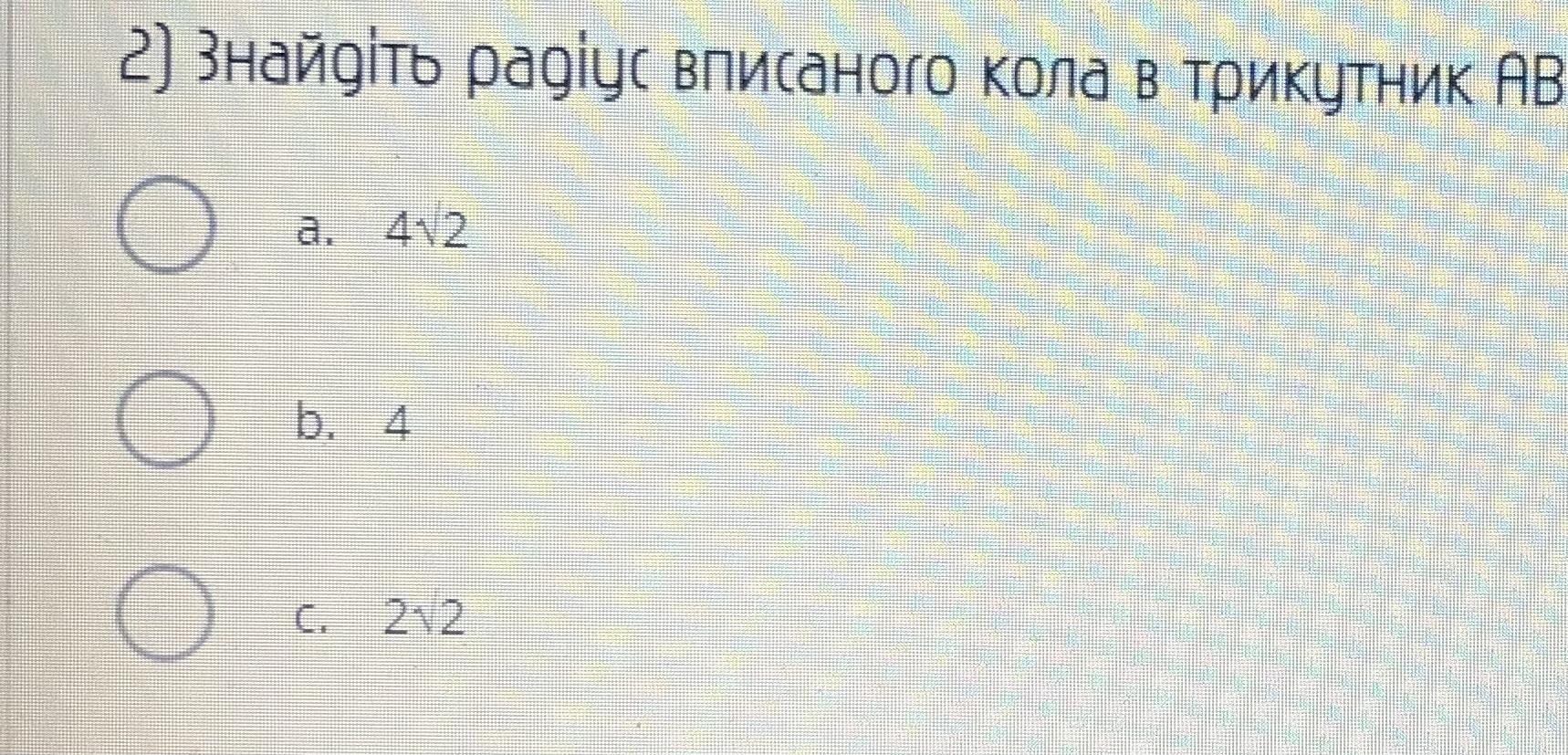
2) Знайдіть радіус вписаного кола
3) Визначие відстань від точки О до площини АКС

Answer 1

Центр равностороннего треугольника - точка пересечения высот/медиан/биссектрис.

BP⊥AC (BP - высота, т.к. проходит через центр O)

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости.

KO⊥ABC => KO⊥AC

Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна плоскости и любой прямой в этой плоскости.

BP⊥AC, KO⊥AC => AC_PKB => AC⊥ON

PK⊥ON (по условию)

=> ON⊥AKC

Расстояние от точки до плоскости - длина перпендикуляра.

ON - расстояние от О до AKC

BP =AB sin60 =8√6 *√3/2 =12√2

Медианы треугольника делятся точкой пересечения 2:1 от вершины.

OP =1/3 BP =4√2 (BP - медиана, т.к. проходит через центр O)

OP - радиус вписанной окружности (O - центр, OP⊥AC)

ON =OP sin45 =4√2 *√2/2 =4