Предмет: Геометрия,
автор: Аноним
Дві сторони трикутника рівні 15см і 12см, а бісектриса трикутника ділить третю сторону на частини, одна з яких на 1см більша за другу. Знайти периметр трикутника
Ответы
Автор ответа:
2
Ответ:
Периметр треугольника равен 36 см.
Объяснение:
Две стороны треугольника равны 15 см и 12 см, а биссектриса треугольника делит третью сторону на части, одна из которых на 1 см больше другой. Найти периметр треугольника.
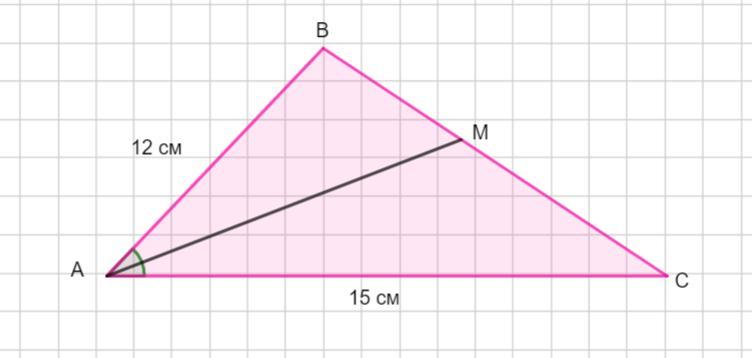
Пусть дан ΔАВС , АВ =12 см, АС =15 см. В треугольнике проведена биссектриса АМ . Воспользуемся свойством биссектрисы треугольника: биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Тогда запишем пропорцию
Пусть ВМ =х см. Тогда МС = (х+1) см. Тогда получим
Тогда ВМ = 4см, а МС =4+1=5 см.
Найдем длину стороны ВС
ВС =ВМ +МС;
ВС = 4+ 5= 9 см.
Периметр треугольника - это сумма длин всех сторон треугольника.
Р= АВ +АС +ВС;
Р= 12+ 15 + 9 =36 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: kamilaslipcenko965
Предмет: Английский язык,
автор: crazyychan228
Предмет: Математика,
автор: masa200977
Предмет: История,
автор: masliyoleksandr
Предмет: Физика,
автор: aleksandramirnaa408