Предмет: Геометрия,
автор: sveta170579
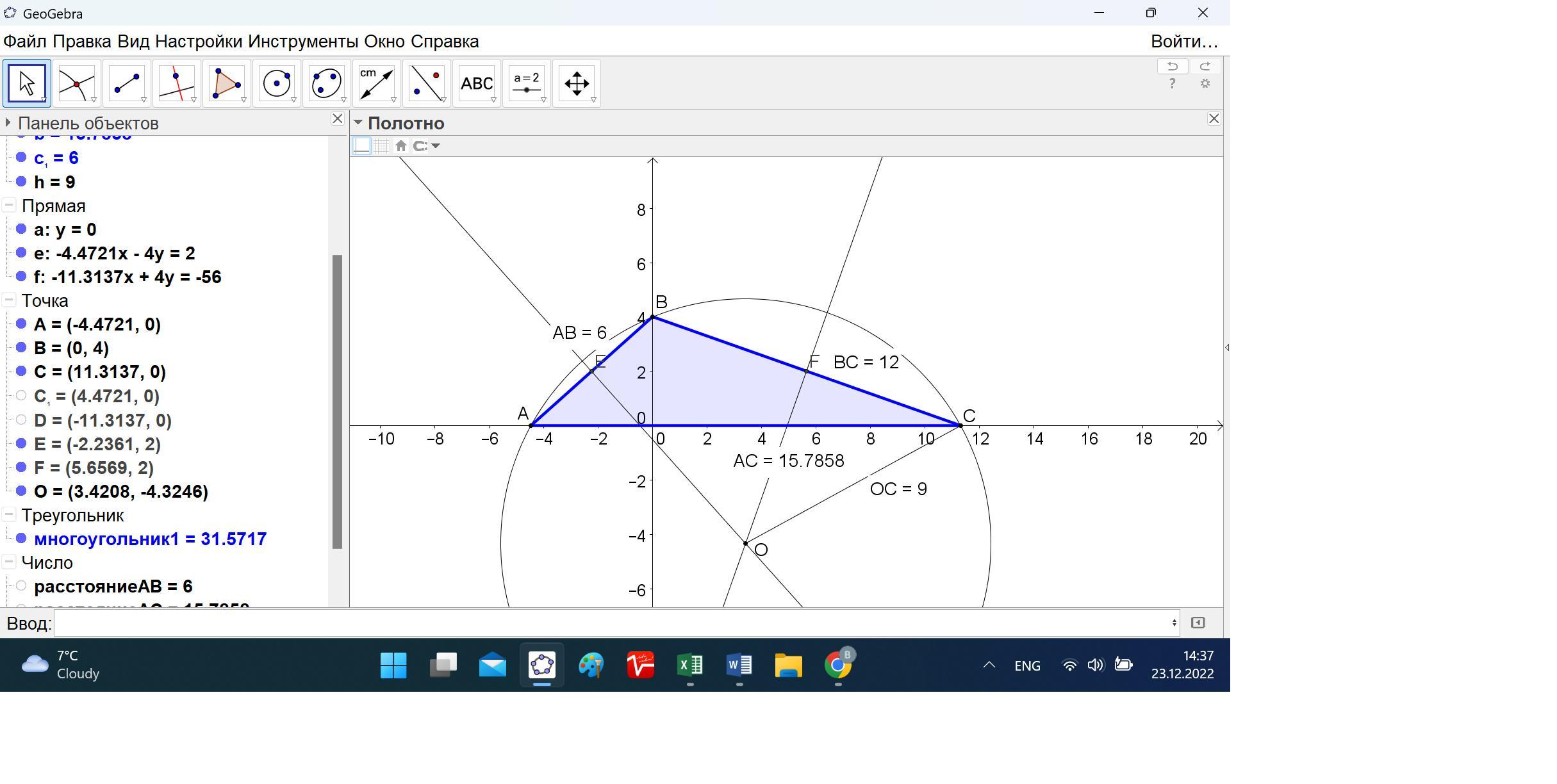
Визначити радіус кола, описаного навколо трикутника, дві сторони якого дорівнюють 6см і 12 см, а висота, проведена до третьої сторони, дорівнює 4 см.
Ответы
Автор ответа:
1
Ответ: 9 см.
Объяснение:
Визначити радіус кола, описаного навколо трикутника, дві сторони якого дорівнюють 6см і 12 см, а висота, проведена до третьої сторони, дорівнює 4 см.
Сначала находим длину третьей стороны с из двух отрезков.
с1 = √(6² - 4²) = √(36 -16) = √20 = 2√5.
с2 = √(12² - 4²) = √(144 -16) = √128 = 8√2.
с = с1 + с2 = 2√5 + 8√2.
Радиус описанной окружности находим по формуле
R = abc/(4S).
Площадь S находим по формуле Герона.
S = √(p(p-a)(p-b)(p-c)).
Полупериметр р = (6 + 12 + 2√5 + 8√2)/2 = 9 +√5 +√2 ≈ 16,89292.
Подставив данные, получаем S = 31,57169 кв. ед.
Тогда R = 6*12*(2√5 + 8√2)/(4*31,57169) = 9.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: vktoriadm
Предмет: Химия,
автор: inkognitous
Предмет: Алгебра,
автор: Gleb1234567899
Предмет: Математика,
автор: valeria1194
Предмет: Биология,
автор: datan0612