помогите пожалуйста дано, решение пожалуйста

Ответы
Ответ: АО=3 см
Объяснение:
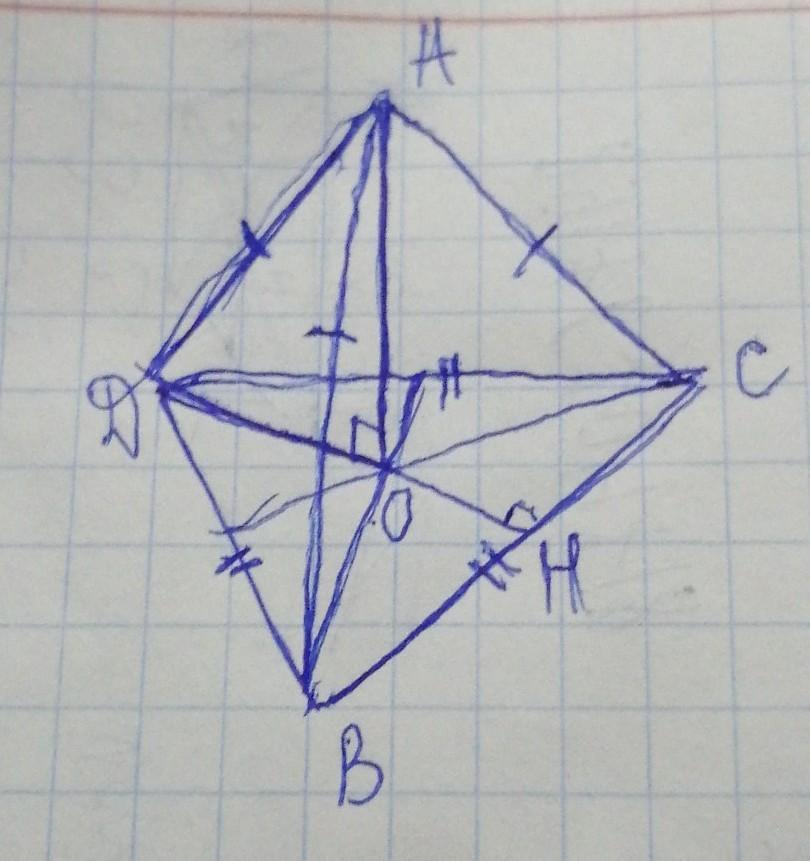
ΔBCD - равносторонний треугольник , о котором сказано в условии.
Так как расстояния от А до вершин треугольника одинаково, то
А проецируется в О- центр описанной окружности вокруг ΔBCD
=> необходимо найти АО. Находить будем из ΔАОВ - прямоугольный
Угол АОВ - прямой.
BCD - равносторонний треугольник . Точка пересечения высот, медиан и биссектрис это одна и та же точка. Она же является центром вписанной и описанной окружности. Поскольку точка пересечения медиан делит их в отношении 2:1, то радиус описанной окружности будет равен 2/3 от длины медианы.
Тогда ОВ это 2/3 высоты ΔBCD . Высота ΔBCD = 4√3*sin 60° =4*3/2=6 cm
2/3 высоты= OB = 6/3*2=4 cm
=> AO²=AB²-BO² =5²-4²=9
АО=3 см
Объяснение:
DB=BC=DC =4√3 см ,т.к ∆DBC -равностороонний.
О - центр,на которую проецируется точка А и является точкой пересечения,высот,биссектрис и медиан .
Высота DH в ∆DBC=a√3/2=4√3•√3/2=6 см.
Медианы в точке пересечения делятся в отношении 2:1 начиная от вершины.
DO=2/3•DH=2/3•6=4 см
АD=AB=AC=5 см
∆АОD - прямоугольный
по теореме Пифагора
АО=√(АD²-DO²)=√(5²-4⁴)=√9=3 см
ответ: 3 см