Решите легким способом пожалуйста

Ответы
Відповідь:
Площадь ромба ABCD равна 12/13 единиц квадратных.
Пояснення:
Ромб ABCD повернули на 90° против часовой стрелки около точки О ( центра ромба - пересечения его диагоналей АС и ВD ) и получили новый ромб A1B1C1D1. Поскольку стороны ромба равны и при повороте диагонали ромба ABCD совпали с диагоналями ромба A1B1C1D1, то в результате объединения двух ромбов мы получили правильный восьмиугольник ALC1MCNA1K ( в виде четырехконечной звезды ), все стороны равны, а углы ∠A = ∠C1 = ∠C = ∠A1 и углы ∠L = ∠M = ∠N = ∠K. В результате пересечения двух ромбов мы получили правильный восьмиугольник B1LBMD1NDK, все стороны равны и все углы равны.
По условию задачи площадь пересечения двух ромбов ( восьмиугольник B1LBMD1NDK - синяя фигура ) составляет 2/3 от площади объединения двух ромбов ( восьмиугольник ALC1MCNA1K - красная и синяя фигуры ).
S(син) = 2/3 S(кр+син)
S(син) / S(кр+син) = 2/3
Таким образом площадь синей фигуры равна двум частям, а площадь красной и синей фигуры равна трем таким же частям ( из них синяя фигура равна двум частям а красная фигура равна одной части ). Следовательно площадь красной фигуры в два раза меньше площади синей фигуры.
Проведем оси симметрии восьмиугольника ALC1MCNA1K: диагонали ромбов АС и А1С1, и точки пересечения двух ромбов KM и LN. В результате мы получили восемь одинаковых красных треугольников ( равных по размерам и следовательно по площади ) и восемь одинаковых синих треугольников.
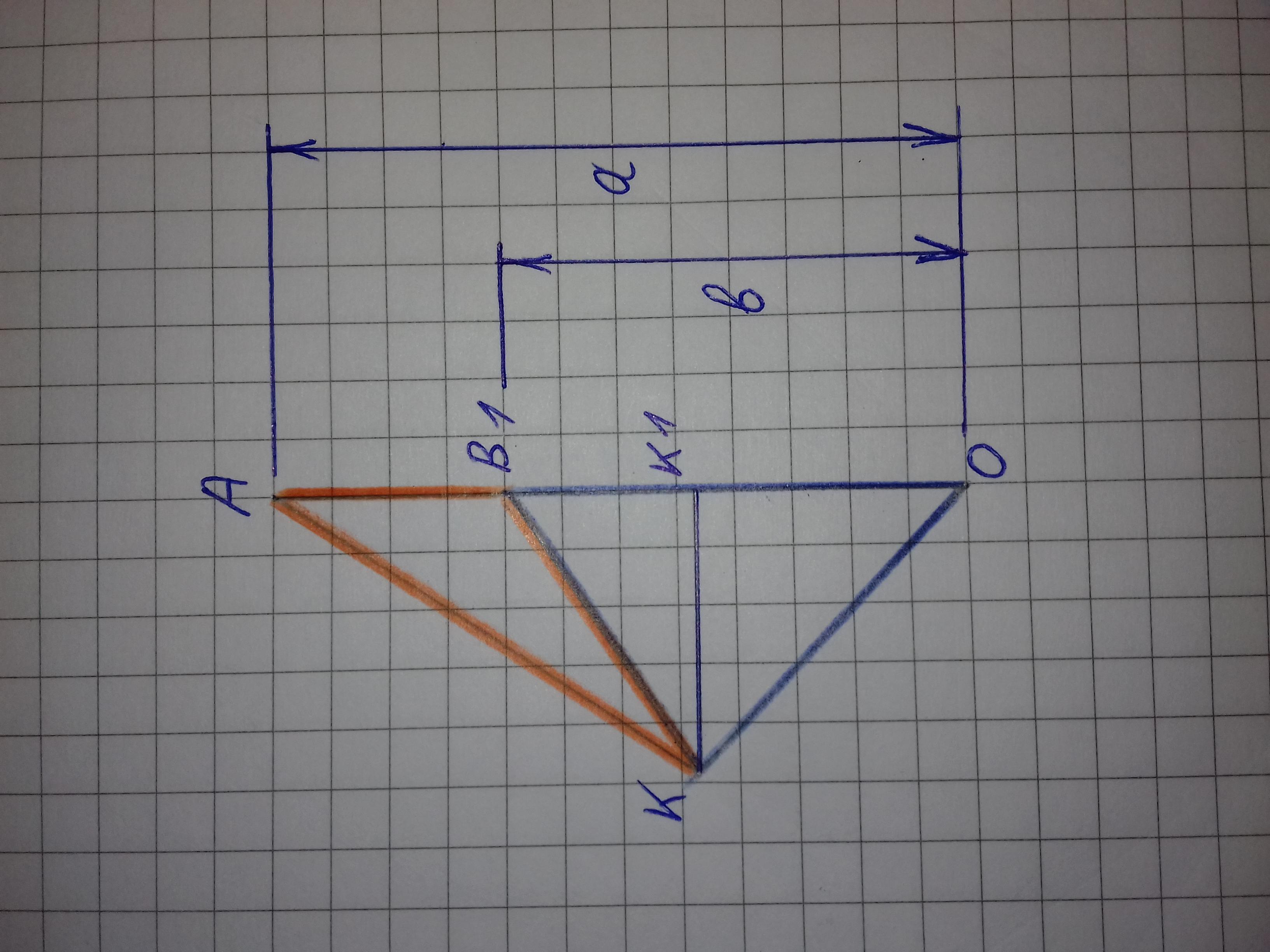
Рассмотрим красный треугольник КВ1А и синий треугольник КВ1О. Составим уравнения для определения их площади. Площадь треугольника равна произведению половины основания на проведенную к этому основанию высоту.
S(КВ1А) = 1/2 × КК1 × АВ1
S(КВ1О) = 1/2 × КК1 × ОВ1
Поскольку, как мы определили выше, площадь красной фигуры в два раза меньше площади синей фигуры, то площадь красного треугольника КВ1А в два раза меньше площади синего треугольника КВ1О.
S(КВ1А) = 1/2 × S(КВ1О)
Подставим формулы для обеих треугольников:
1/2 × КК1 × АВ1 = 1/2 × 1/2 × КК1 × ОВ1
После сокращения одинаковых множителей получаем:
АВ1 = 1/2 × ОВ1
Введем следующие обозначения:
большая диагональ ромба АС = А1С1 = 2а;
меньшая диагональ ромба BD = B1D1 = 2в.
Значит половины диагоналей ромба равны:
ОА = ОА1 = ОС = ОС1 = а
ОВ = ОВ1 = ОD = ОD1 = в
Диагональ ОА = АВ1 + ОВ1
Как мы определили выше:
АВ1 = 1/2 × ОВ1
Тогда:
ОА = АВ1 + ОВ1 = 1/2 × ОВ1 + ОВ1 = 1,5 ОВ1
а = 1,5 × в
Рассмотрим треугольник АВО - он прямоугольный ∠АОВ = 90°, ОА = а = 1,5 × в, ОВ = в, а АВ = 1 ( по условию задачи ). По теореме Пифагора:
1² = а² + в²
1² = (1,5 × в)² + в²
1 = 2,25в² + в² = 3,25в²
в² = 1 / 3,25
в = 1 / √3,25
а = 1,5 / √3,25
Площадь ромба определяется как половина произведения его диагоналей.
S(ABCD) = 1/2 × АС × BD = 1/2 × 2а × 2в = 2ав
Подставим в формулу найденные значения а и в, получаем:
S(ABCD) = 2 × 1 / √3,25 × 1,5 / √3,25 = 3/3,25 = 12/13 единиц квадратных.