Предмет: Геометрия,
автор: xiolli
СРОЧНО!!!!!!
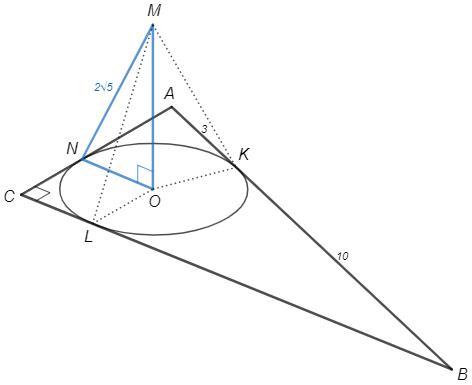
Точка М не належить площині трикутника ABC (кутACB = 90°) і розташована на відстані 2√5 см від кожної з прямих, що містять його сторони. Проекцією точки М на площину ABC е точка О, яка належить даному трикутнику. Точка дотику гі- потенузи АВ до кола, вписаного в трикутник ABC, ділить й на відрізки завдовжки 3 см і 10 см. Знайдіть відстань від точки М до площини ABC.
Ответы
Автор ответа:
3
Расстояния от М до сторон треугольника равны, следовательно равны их проекции.
То есть расстояния от O до сторон треугольника равны.
O - центр вписанной окружности ABC.
Достаточно найти радиус, и мы сможем найти MO по т Пифагора.
Пусть K, L, N - точки касания.
Отрезки касательных из одной точки равны.
AN=AK=3, BK=BL=10, CL=CN
CNOL - квадрат (радиусы в точки касания перпендикулярны касательным и равны)
CL=CN=r
AC^2+BC^2=AB^2 => (r+3)^2 +(r+10)^2 =13^2 => r=2
ON=r=2, MN=2√5
MO=√(MN^2-ON^2)=4 (см)
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: kuprijcuktatana41
Предмет: Химия,
автор: okok8888
Предмет: Українська мова,
автор: mspidenko
Предмет: Математика,
автор: albinahan8