Предмет: Математика,
автор: dasagrubova
Доведіть що при всіх допустимих значеннях а значення виразу не залежить від а
Приложения:
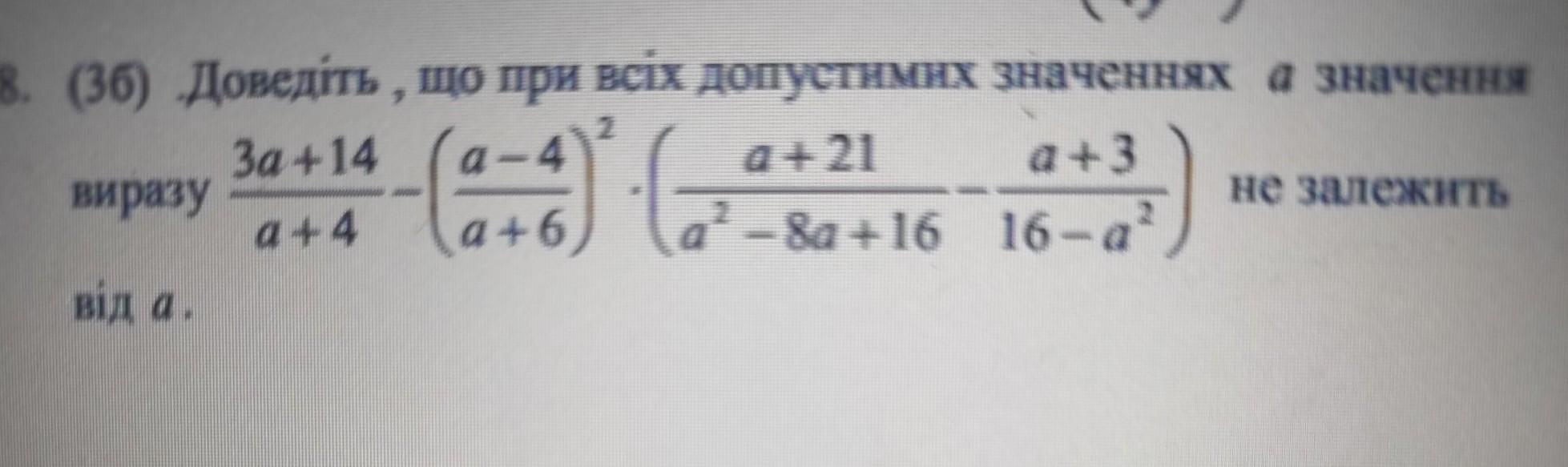
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
=> выражение не зависит от а при всех допустимых а
Похожие вопросы
Предмет: Українська мова,
автор: klsfsdlkfskljdk
Предмет: Русский язык,
автор: azatmakisev2
Предмет: Литература,
автор: vladprostakisin62
Предмет: Информатика,
автор: roman0va1607
Предмет: Українська мова,
автор: makscozda307