Question

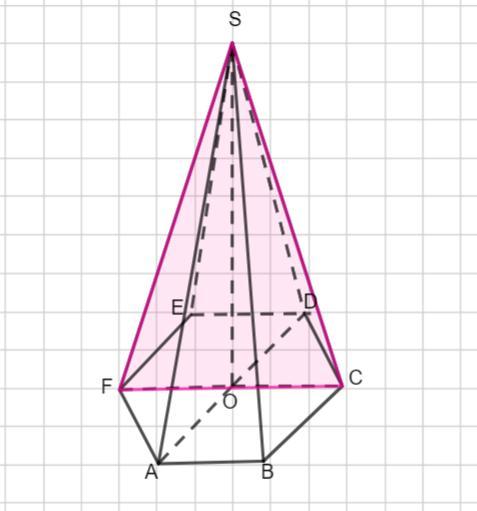
Высота правильной шестиугольной пирамиды равна 8 см, а сторона основания 4 см. Вычислите площадь большего диагонального сечения пирамиды.

Answer 1

Ответ:

Площадь большего диагонального сечения пирамиды равна

32 см².

Объяснение:

Высота правильной шестиугольной пирамиды равна 8 см , а сторона основания 4 см. Вычислить площадь большего диагонального сечения пирамиды.

Пусть дана правильная  шестиугольная пирамида SABCDEF

Высота  SO = 8 см, в основании шестиугольник, все стороны которого равны 4 см.

Найдем площадь большего диагонального сечения, то есть площадь треугольника FSC  , основание которого равно большей диагонали FC правильного шестиугольника ABCDEF.

Большая диагональ правильного шестиугольника в 2 раза больше стороны шестиугольника . Значит ,

$FC = 2\cdot 4 = 8$ см.

Найдем площадь данного треугольника как полупроизведение стороны на высоту, проведенную к данной стороне.

$S= \dfrac{1}{2} \cdot FC \cdot SO ;\\\\S= \dfrac{1}{2} \cdot 8 \cdot 8=4\cdot 8=32$ cм²

Тогда площадь большего диагонального сечения пирамиды равна 32 см².

#SPJ1