Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу
Приложения:
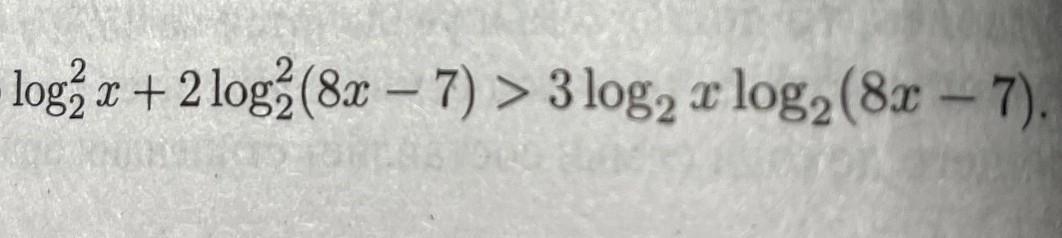
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ:
Неравенство имеет вид
Здесь Поэтому получаем
Важный момент: основание логарифмов больше 1, а логарифмическая функция в случае основания большего 1 возрастает, что приводит к тому, что на области определения
Иными словами, знак выражения совпадает со знаком выражения
Поэтому наше неравенство равносильно (на ОДЗ!) неравенству
Скобку (x-49/64) я отбросил, поскольку на ОДЗ она положительна.
Ответ:
Похожие вопросы
Предмет: Математика,
автор: arr32572
Предмет: Литература,
автор: anastasiadondoha16
Предмет: Право,
автор: misanaprokpenko481
Предмет: Биология,
автор: Аноним
Предмет: Музыка,
автор: anastasia501079